Una de las preguntas/ejercicios que hacemos en el curso online de FAGUS consiste en mostrar una sección con unos esfuerzos aplicados en el Axis Point y en la que además queremos tener en cuenta el efecto del cortante. El alumno debe saber pasar esos esfuerzos al centro de gravedad, con las transformaciones necesarios para realizar el cálculo.
Un alumno nos pregunta que "por qué no se incrementa el momento My de cálculo si aparece un axil de tracción que discurre por la armadura". La pregunta es muy interesante y nos lleva a escribir este artículo en el que volvemos a insistir en:
el fenómeno del cortante como un "viaje de las cargas hacia los apoyos a través de la analogía de la celosía".
en la forma en la que FAGUS trabaja con el cortante a través de las paredes de cortante
en los 3 modelos V-T de cálculo que FAGUS propone para trabajar con el cortante y la torsión.
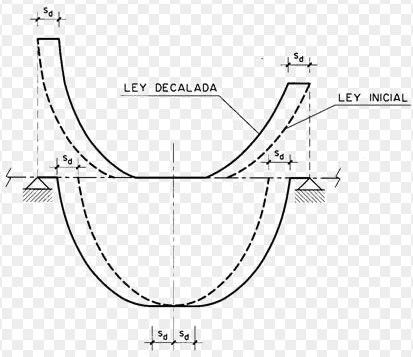
El esfuerzo cortante en una viga se desarrolla siempre y cuando haya una variación de la ley de momentos flectores en la misma. Dicho de otra forma, la ley de esfuerzos cortantes está ligada a la ley de momentos flectores y no se entiende una sin la otra.
Por efecto del trabajo en celosía se modifican los axiles en la cabeza de la viga. Las armaduras longitudinales a flexión han de ser capaces de soportar un incremento de tracción respecto a la producida por Md, para ello se desplaza la ley de flectores un canto útil d hacia la parte más desfavorable, así se tiene en cuenta el efecto de la fisuración oblicua por cortante (el valor d está del lado de la seguridad).
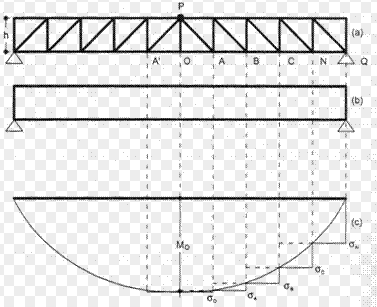
La estructura interna en forma de celosía que se genera a partir de las bielas comprimidas y de los tirantes que conforman las armaduras de cortante (cercos verticales) y las armaduras longitudinales será a la que equilibre todas las fuerzas que en ella intervengan.
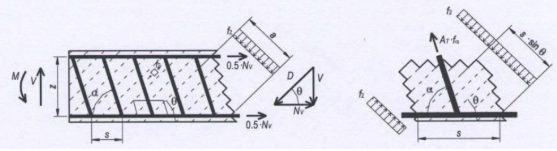
Teniendo en cuenta lo anterior vamos a explicar cómo realiza FAGUS la transformación de los esfuerzos centrándonos en el cortante, ya que es el tema del que trata la pregunta.
En el ejemplo presentado en el vídeo del curso tenemos una sección rectangular que, como es lógico, es una sección simétrica en los dos ejes. La transformación de los esfuerzos teniendo en cuenta el cortante dependerá fundamentalmente de dos cosas:
a) de la geometría de la sección.
En el ejemplo, al tener una sección rectangular tendremos el cdg situado justo a la mitad del canto de la misma. Además nuestra pared de cortante que resiste el cortante vertical Vz tiene una altura igual a dicho canto, lo que hace que el centro de cortante de esa pared coincida con el cdg de la sección. El resultado de la transformación es un cortante igual al introducido y un axil en el punto del que hablamos sin excentricidad con respecto al cdg de la sección y, en consecuencia, sin generar momento.
Todo esto es diferente si en lugar de una sección simétrica respecto a un eje horizontal que pase por el cdg tenemos una asimétrica con respecto a dicho eje. En ese caso existe una distancia entre el cdg de la sección y el centro de cortantes de la pared de cortante. Tomemos la siguiente sección:
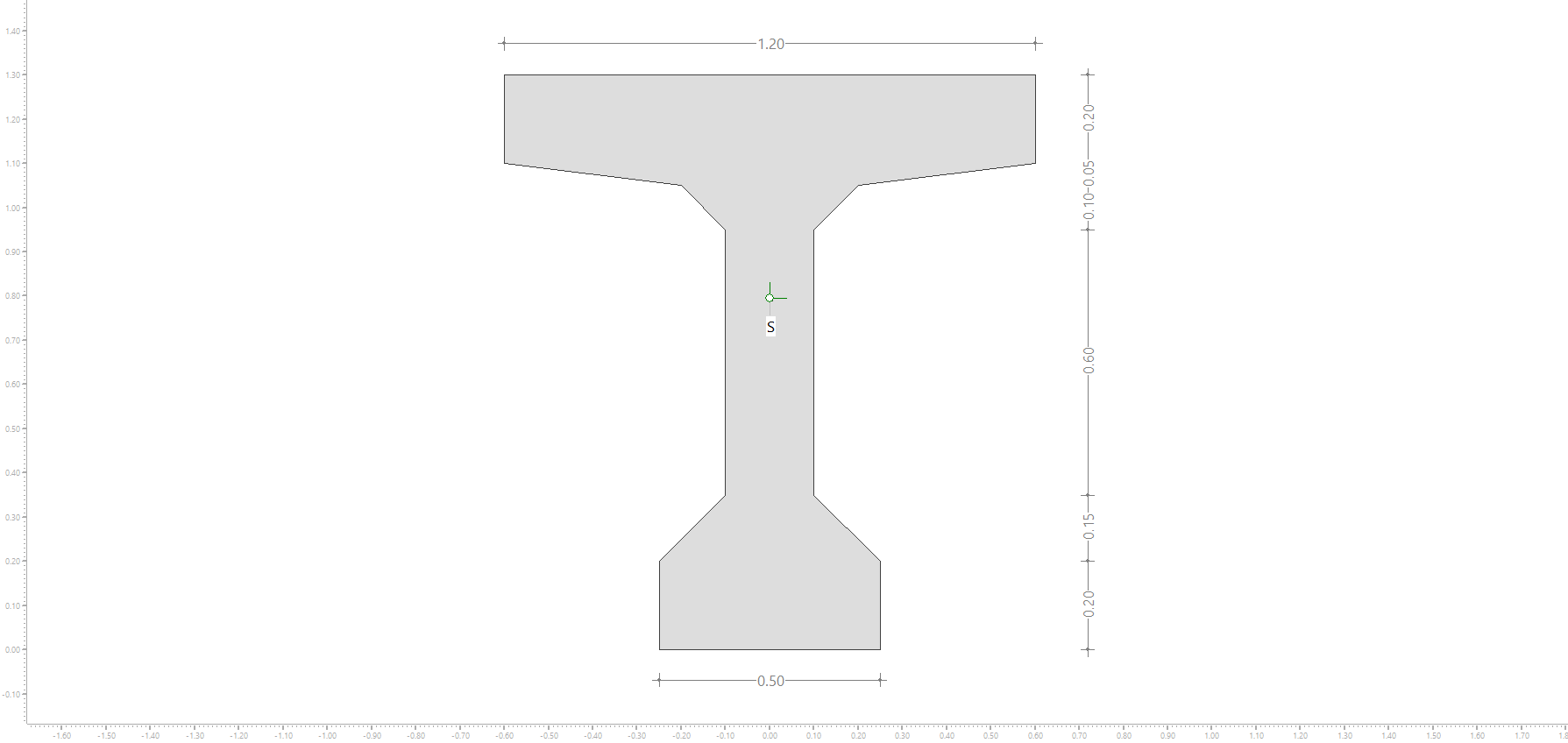
Tenemos que el cdg de la sección se sitúa a 0.80 m de la base de la misma.
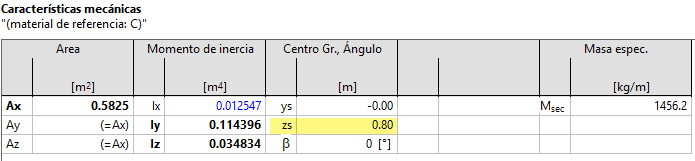
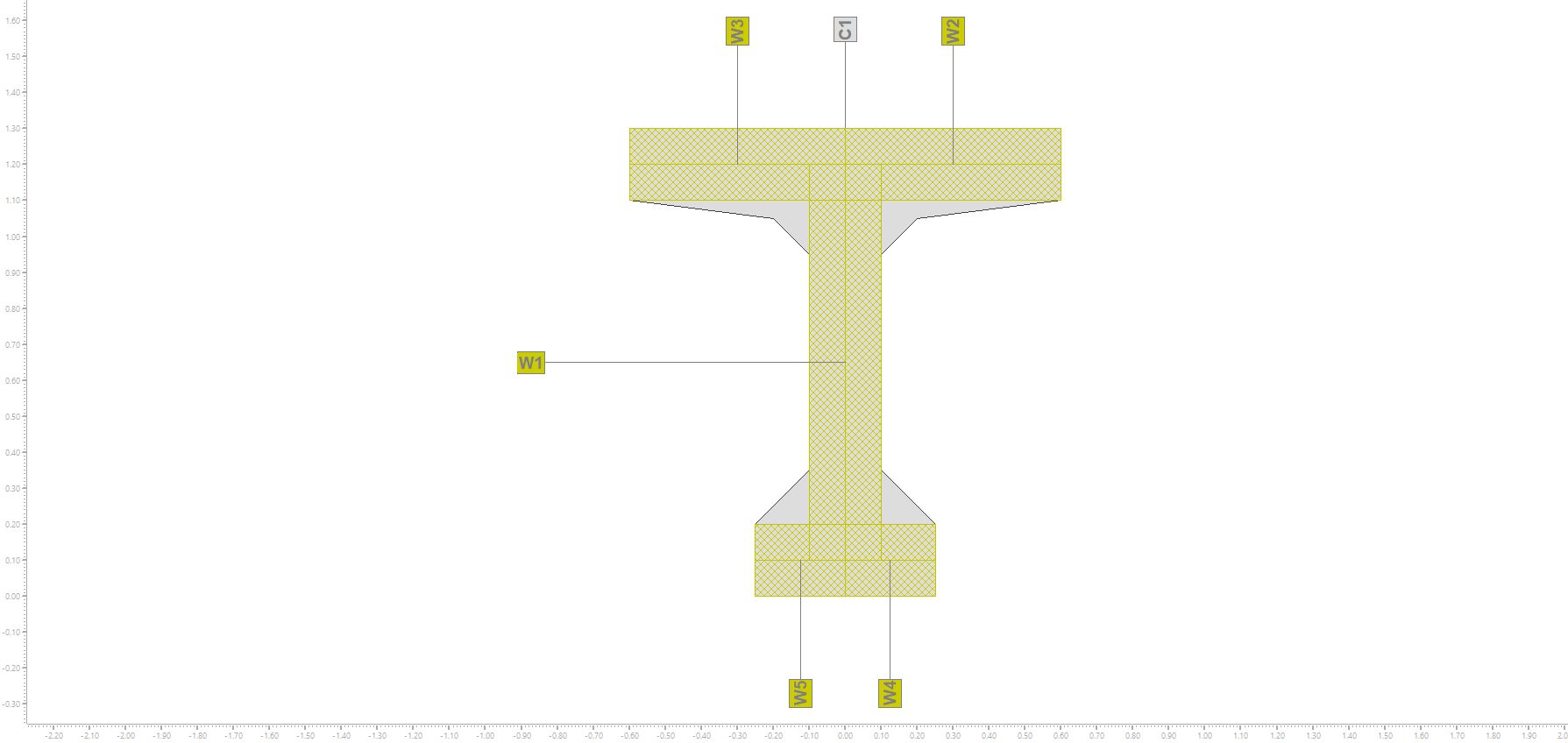
En esta sección podemos definir las siguientes paredes de cortante:
Si nos fijamos en la pared de cortante vertical, que tiene una altura comprendida entre la línea media de cada una de las alas e igual a 1.1 m, tendríamos que su centro de cortante estaría en el punto medio, es decir, a 0.55 m de cualquiera de sus extremos. Esto supondría que habría una excentricidad con respecto al cdg de la sección de 0.15 m.
Si introducimos un cortante de 10 kN y consideramos una inclinación de las bielas de comprimidas de 45º cabría esperar la aparición e un axil de 10 kN situado en dicho centro de la pared de cortante vertical (mismo valor que el cortante por esos 45º).
En esta sección podemos definir las siguientes paredes de cortante:
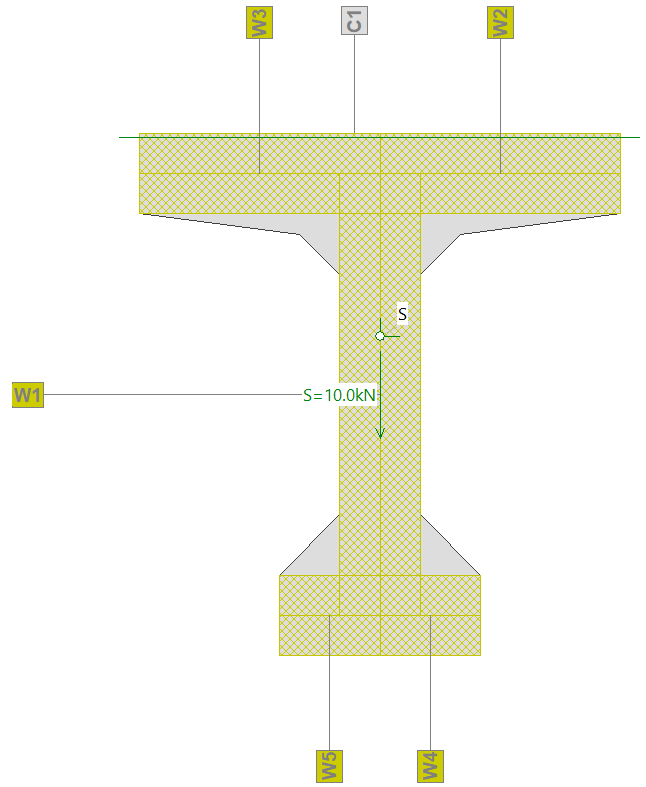
Este axil de 10 kN multiplicado por la excentricidad hasta el cdg de la sección resulta un momento de 10*0.15 = 1.5 kNm.
Si miramos la transformación de los esfuerzos que hace FAGUS:

Observamos ese incremento en el My.
Esto se explica en el siguiente apartado del manual de FAGUS:

b) del modelo V-T seleccionado
Para que lo descrito en el apartado a) ocurra es muy importante elegir el modelo V-T de forma correcta. En este punto nos gustaría recomendarte la lectura de nuestro artículo que trata este tema y que está disponible en nuestro Help Center y al que puedes acceder a través del siguiente enlace:
"¿Cómo elegir el tipo de modelo cortante-torsor (V-T) que mejor se adapta al caso de estudio?"
En este caso el modelo ideal a elegir será el Tipo A, ya que en secciones como esta el programa decidirá que pared resistirá el esfuerzo cortante introducido en función de la geometría. El modelo Tipo B también sería válido pero seremos nosotros los que debamos especificar que pared trabaja para cada esfuerzo.
El modelo automático hace que las paredes existentes en las alas se lleven algo del cortante vertical debido al circuito de cortante que introduce dentro de cada pared. Esa pequeña parte de cortante vertical no la muestra el programa y no podemos controlarla por lo que este tipo de modelo no es el más adecuado para estas secciones donde está claro que nunca interesará que las alas trabajen para un cortante Vz.
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS-7 avalado por CUBUS AG (licencia de estudiante disponible).

Quizás también te interese:


















¿Ya tienes cuenta? Haz login