Si se introduce un coeficiente de fluencia φ mayor que cero en los parámetros de análisis, el análisis se lleva a cabo considerando este fenómeno característico del hormigón. En consecuencia, la deformación total ε para todas las fibras de hormigón se divide en una parte elástica εe y la parte correspondiente a la fluencia εcc, de acuerdo con las relaciones siguientes:
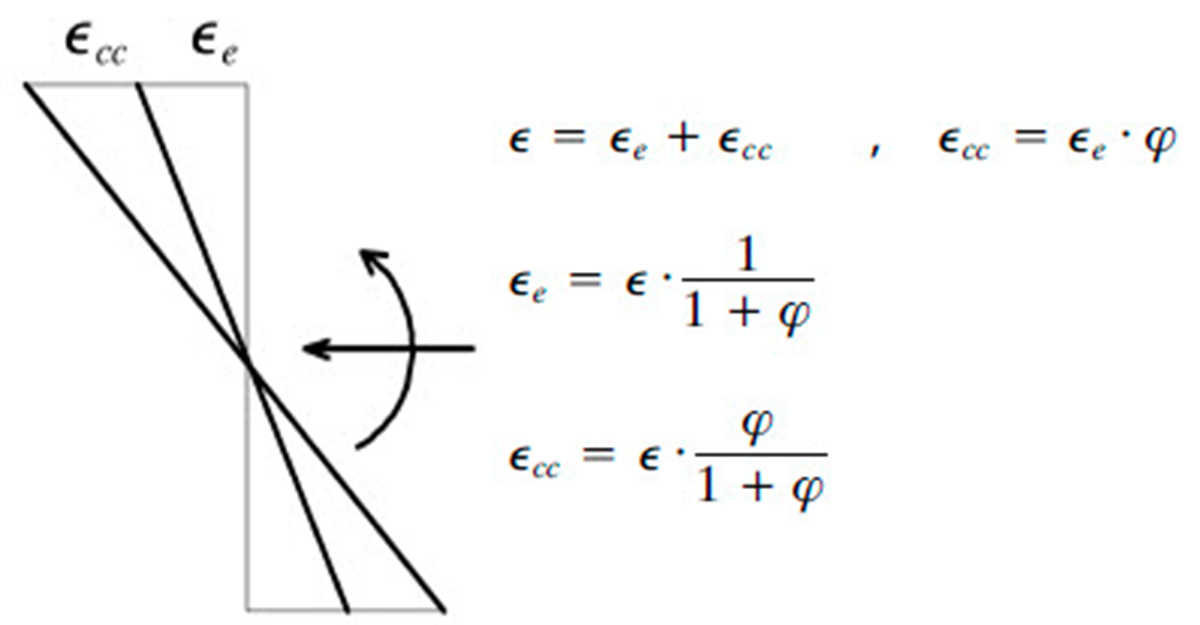
Si nos fijamos en el caso particular de la determinación de las tensiones, así como para la verificación de las deformaciones máximas, se tendrá en cuenta la parte elástica εe.
En la presentación de resultados gráficos siempre se muestra la parte elástica de las deformaciones. Esto supone que, cuando se estén verificando los resultados numéricos que proporciona FAGUS, se deberán esperar distintos valores de ε para el acero y el hormigón en un mismo punto. Veamos esto con un sencillo ejemplo.
En la sección siguiente, introducimos una serie de puntos de resultados para evaluar las deformaciones del acero y del hormigón en la posición de las armaduras:
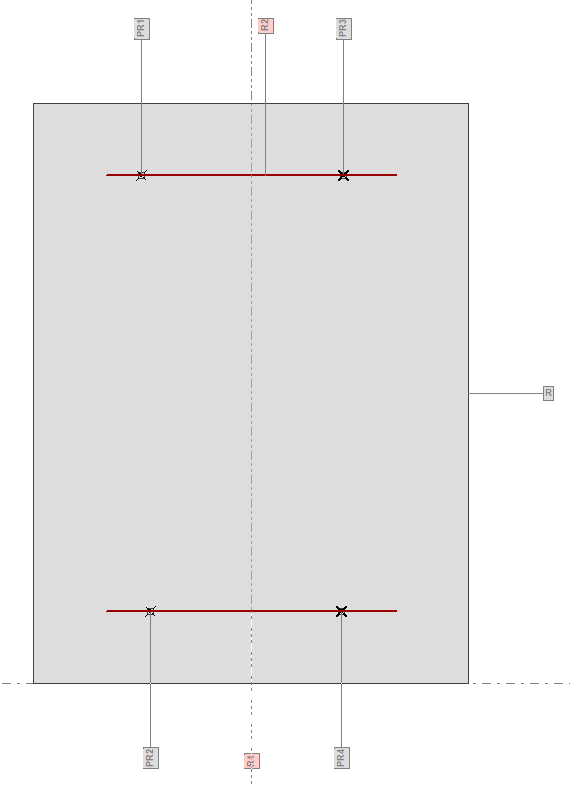
PR1, PR2 = puntos de resultados referidos al material hormigón.
PR3, PR4 = puntos de resultados referidos al material acero.
Veamos a continuación qué resultados obtenemos sin considerar un coeficiente de fluencia (φ=0) y considerándolo (aunque se trate de un coeficiente de fluencia muy grande, en este ejemplo consideramos φ=4 para poner de manifiesto las diferencias).
A.1- Sin coeficiente de fluencia (φ=0)
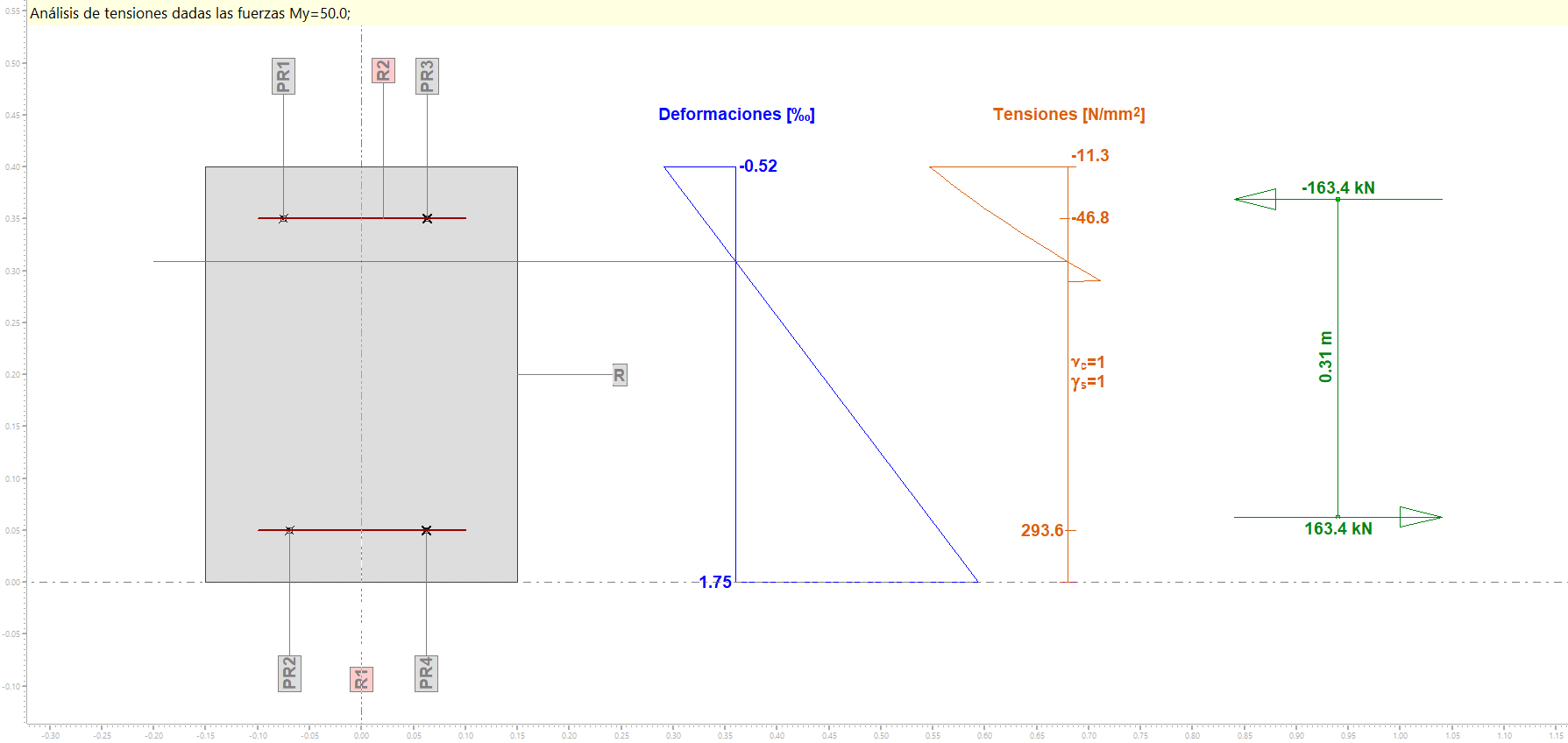


A.2- Considerando un coeficiente de fluencia (φ=4)
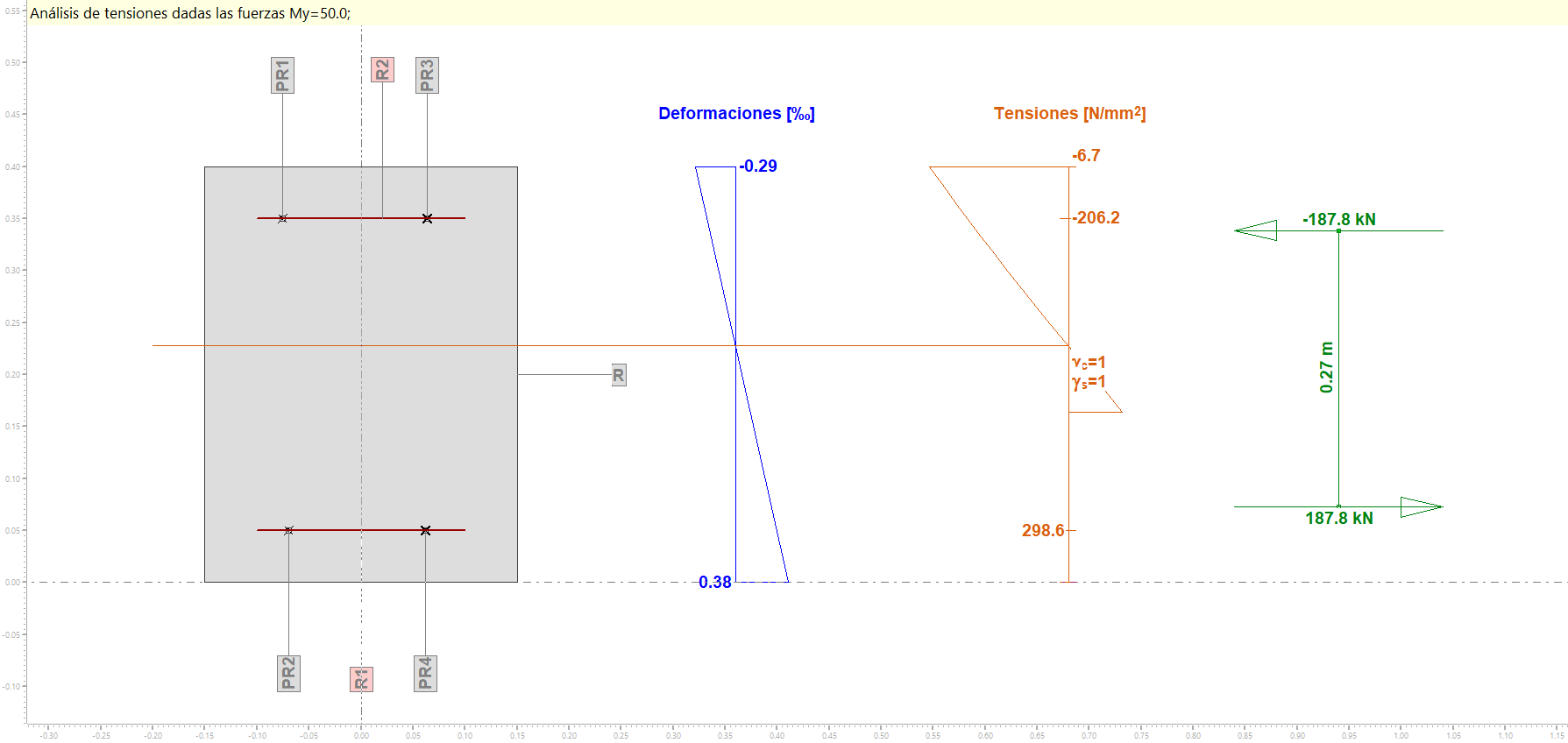


CONCLUSIONES A.1-A.2:
Atendiendo a los resultados obtenidos en las tablas "Punto de resultados" vemos que, en el caso A.1, las deformaciones obtenidas para hormigón y acero en un mismo punto coinciden, mientras que en el caso A.2 se cumplen las relaciones entre las deformaciones en un mismo punto, presentadas al inicio de este artículo:
εPR3 (acero R2) = -0.21 + (-0.21)·4 = -1.05 por mil
εPR4 (acero R1) = 0.30 + 0.30·4 = 1.5 por mil
Las deformaciones de las fibras extremas del hormigón superior es inferior son -0.29 y 0.38 respectivamente (lo cual tiene sentido, ya que las deformaciones del hormigón a la altura de las armaduras eran -0.21 y 0.30, lo que nos lleva, siguiendo una la ley lineal, a valores de -0.29 y 0.38 en los extremos). Como hemos comentado anteriormente, estas deformaciones corresponden a la parte elástica de la deformación total εe. Las deformaciones en el acero coinciden exactamente con las obtenidas en los puntos de resultados para la combinación con fluencia y representan las deformaciones totales εt=εe+εcc.
NOTA: en ocasiones hay diferencias insignificantes que se deben a los decimales tomados en el cálculo. Es posible y muy sencillo seleccionar el número de decimales con el que queremos ver cada resultado (deformaciones en este caso).
Queremos hacer hincapié en que se debe tener cuidado a la hora de interpretar los resultados de deformaciones cuando se introduzca un valor del coeficiente de fluencia distinto de cero ya que, como acabamos de comprobar, el programa nos mostrará únicamente la parte elástica de la deformación para el hormigón, y la deformación total para las armaduras.
El coeficiente de fluencia afectará también a los resultados relativos a la verificación de la abertura de fisura.
Atendiendo al manual de FAGUS:
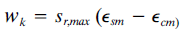
donde:
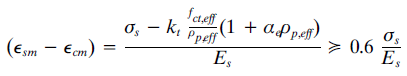
En la fórmula anterior vemos que aparece el término de la tensión en las armaduras traccionadas σs. Este término se verá afectado, como es lógico, cuando se considere un φ>0 ya que supondrá una mayor deformación y, en consecuencia, un incremento de esta tensión.
Si realizamos la verificación de la abertura de fisuras en la sección del ejemplo anterior introduciendo unos esfuerzos N=-100 kN y My=100 kNm vemos que, para φ=0:
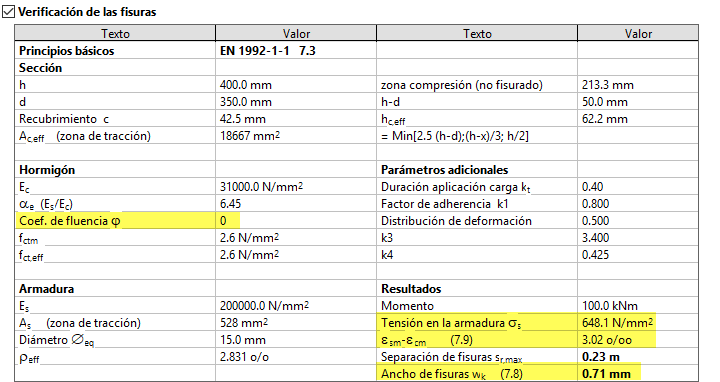
Si realizamos la misma verificación considerando φ=4:
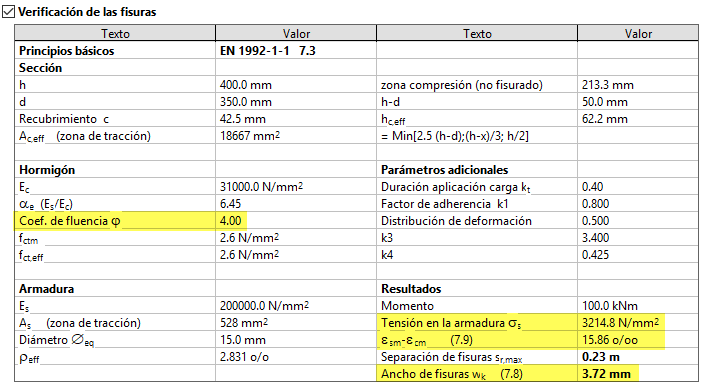
Vemos como el incremento de tensión en las armaduras traccionadas supone un incremento de la abertura de fisura.
La tensión en las armaduras traccionadas mostrada en el segundo cuadro de 3214.8 N/mm2, corresponde con el alargamiento total en esas armaduras (ε=εe+εcc) para esos esfuerzos, que sería del 16.1 por mil, como se puede observar en la siguiente figura:

σ = E·ε = 200000 · 0.016074 (0.0161 en la tabla por el redondeo) = 3214.8
Y que, como ya hemos visto a lo largo de este artículo, es el valor que se obtiene haciendo:
εPR4 = 3.2 + 3.2 · 4 = 16.1 por mil
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS-7 avalado por CUBUS AG (licencia de estudiante disponible).

Quizás también te interese:


















¿Ya tienes cuenta? Haz login