La implementación de un cálculo dinámico en STATIK se lleva a cabo de forma sencilla a través de un cuadro de diálogo muy intuitivo. No obstante, creemos importante explicar con detalle el modo en el que este programa lleva a cabo la superposición de los modos de vibración y cómo se combinan los resultados de las diferentes direcciones de excitación sísmica con el objetivo de diseñar una estructura.
El cuadro de definición del "Cálculo del espectro de respuesta" tiene el siguiente aspecto:
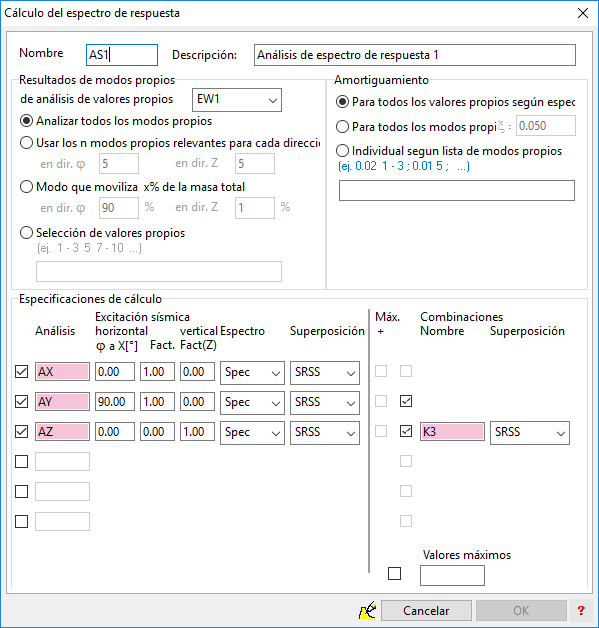
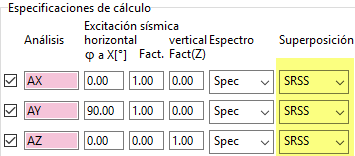
En este artículo nos vamos a centrar en las funcionalidades recogidas en la parte inferior del mismo:
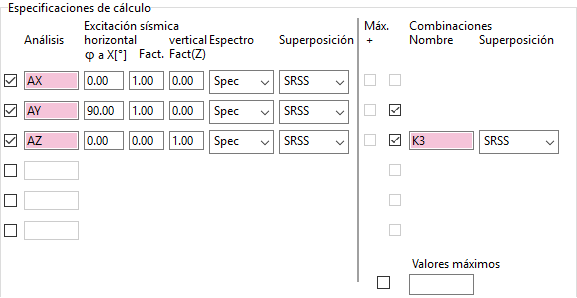
En la parte izquierda de definición de las especificaciones de cálculo vemos que existe una última columna llamada "Superposición". Aquí es donde elegiremos el método de superposición de los modos de vibración. En la parte derecha disponemos de las opciones necesarias para definir la combinación de resultados de las diferentes especificaciones de cálculo definidas a la izquierda. También vemos un desplegable en el que elegiremos el método de combinación que deseemos.
- MÉTODOS DE SUPERPOSICIÓN DE MODOS DE VIBRACIÓN
Como las amplitudes máximas de los modos de vibración considerados no ocurren todas al mismo tiempo, el problema se reduce a saber cómo deben combinarse los resultados derivados de estos modos para obtener un resultado adecuado con el propósito de llevar a cabo un diseño ya que una simple suma sería demasiado conservadora.
A nivel conceptual diremos que no pueden superponerse las formas de los modos de vibración en sí mismas, sino sólo los resultados escalares calculados para cada modo, como por ejemplo las solicitaciones o las componentes de las reacciones en un determinado punto de la estructura.
Para explicar los distintos métodos de superposición que ofrece STATIK seguiremos la siguiente nomenclatura:
E: el resultado de interés, por ejemplo, la fuerza normal en un punto de la estructura.
Ei: el valor de E debido a Ai,max (desplazamientos máximos del modo i).
Emax: el valor máximo de E (todos los modos considerados combinados).
1) Sumatorio de las contribuciones en valor absoluto
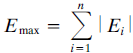
Este método no tiene ninguna importancia desde un punto de vista práctico ya que, como hemos comentado anteriormente, proporciona resultados demasiado conservadores.
Si tomamos como ejemplo la siguiente estructura sencilla compuesta por una pila empotrada en su base y un pequeño dintel:

Y a la que somete a una excitación sísmica en las 3 direcciones (X, Y, Z) en las que llevamos a cabo una superposición de los modos con el método del sumatorio para todas ellas:
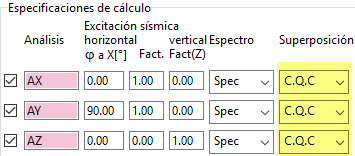
Por ejemplo, la ley de momentos My obtenida para la primera especificación de cálculo AS1_AX es:
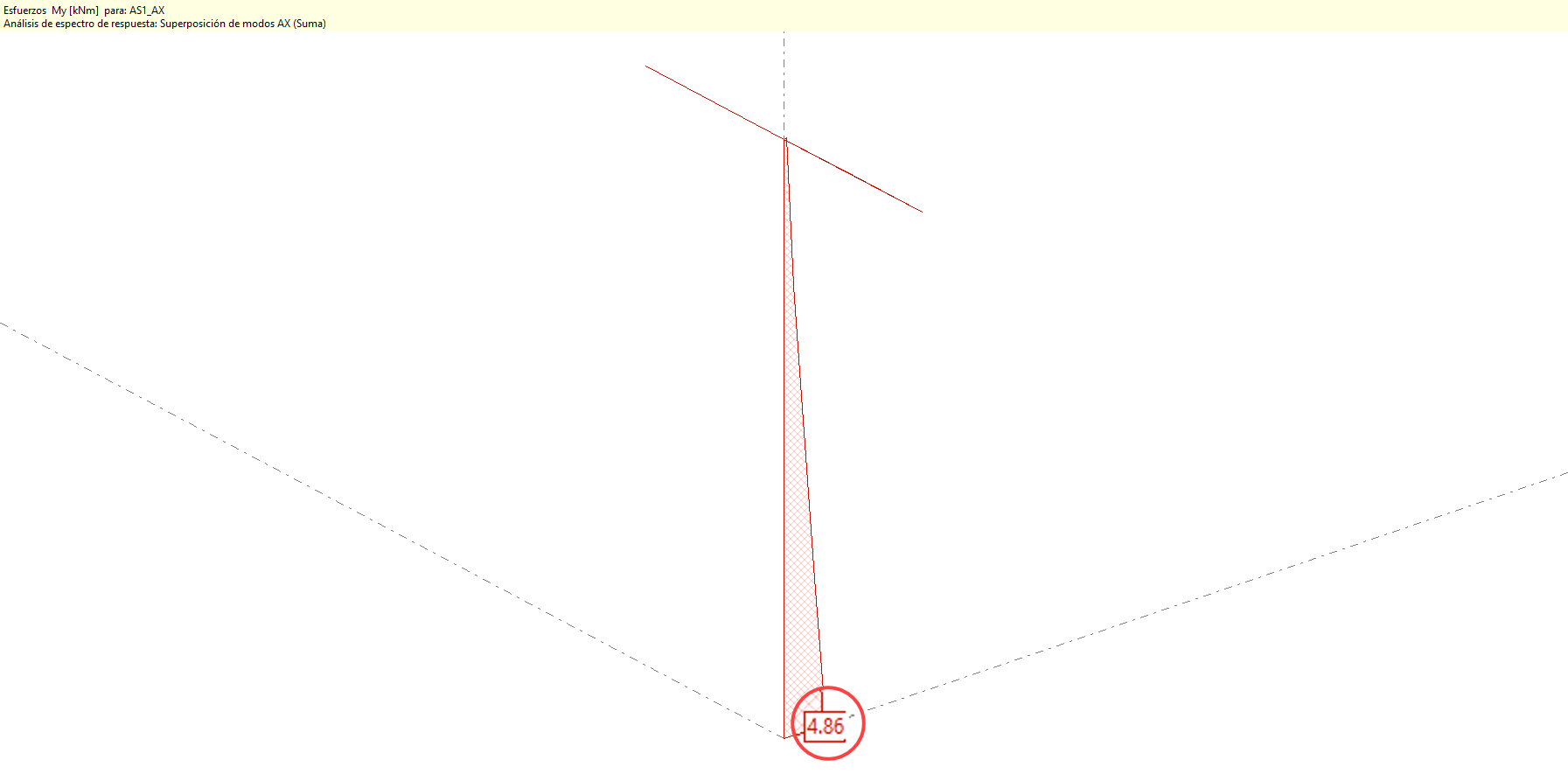
El valor del momento de 4.86kNm en la base del soporte se obtiene como suma de los valores absolutos de los momentos obtenidos para cada uno de los modos de vibración analizados.
La operación que hace con momentos obtenidos para los modos analizados (5 en este caso) es:
My = E1+E2+E3+E4+E5 = 4.86 kN
2) Método SRSS (Square-Root-of-Sum-of-Squares).
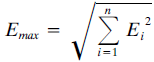
Este método asume que todas las respuestas modales pueden considerarse de forma independiente unas de otras. En caso contrario, este método no sería conservador. De acuerdo con el Eurocódigo 8, dos modos pueden considerarse independientes entre sí si sus periodos Ti y Tj (Ti<=Tj) satisfacen la condición Ti<=0.9*Tj.
Veamos qué ocurre si obtenemos el mismo valor del momento del ejemplo anterior empleando este método:

El valor obtenido es ahora de 4.79kNm, ligeramente inferior al obtenido con el método anterior. En este caso, el resultado se obtiene haciendo la raíz cuadrada de la suma de los cuadrados de los momentos obtenidos para cada uno de los modos de vibración analizados.
La operación que hace con momentos obtenidos para los modos analizados (5 en este caso) es:
My = (E1^2+E2^2+E3^2+E4^2+E5^2)^1/2 = 4.79 kN
3) Combinación cuadrática completa (C.Q.C)
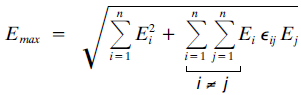
Si no se cumple la condición de independencia de los modos para poder aplicar el método SRSS, deberá aplicarse el método C.Q.C.
Si el segundo término de la expresión bajo la raíz se va reduciendo, el método acaba convergiendo al método SRSS. Si nos fijamos en la expresión de los coeficientes de correlación:
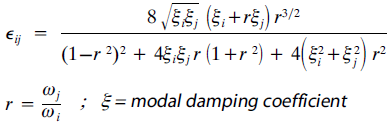
Dicha convergencia del método al SRSS, se producirá si el amortiguamiento disminuye, si la relación r entre las dos frecuencias correlativas es grande o si el producto Ei * Ej de los modos con frecuencias dependientes es muy pequeño.
Con este método, el valor del momento que obtenemos en nuestro ejemplo es:

Vemos que el valor es idéntico al obtenido con el método SRSS. Esto se debe a que se ha producido la convergencia explicada por las características específicas de este modelo en concreto, pero no será así siempre.
- COMBINACIÓN DE RESULTADOS DE LAS DIFERENTES DIRECCIONES DE EXCITACIÓN
Un análisis de espectro de respuesta se lleva a cabo siempre para una determinada dirección de excitación, por ejemplo la dirección X. Para un análisis completo, al menos deberá considerarse una excitación para la dirección Y (perpendicular a la X) e incluso podría tenerse en cuenta una cierta excitación vertical en el eje Z.
Los efectos de la excitación en las distintas direcciones se denotan como EEx, EEy, EEz y pueden combinarse utilizando uno de los siguientes métodos:
a) Suma de los valores absolutos de los resultados
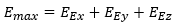
Muy conservador.
b) Método SRSS (Square-Root-of-Sum-of-Squares).

Método estándar.
c) Método del Eurocódigo 8.
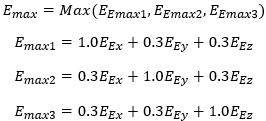
Veamos, a partir del ejemplo sobre el que estamos desarrollando la explicación, las diferencias en los resultados cuando se aplica cada uno de los métodos de combinación. Nos fijaremos en este caso en los resultados del My en el punto de encuentro entre el soporte y el dintel.
Método A) Suma de los resultados obtenidos para cada dirección:
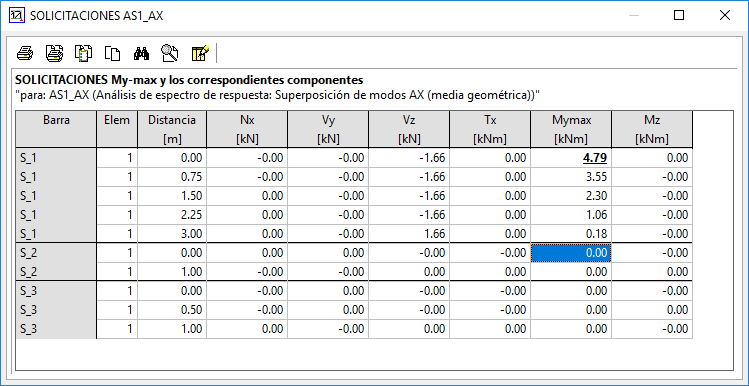
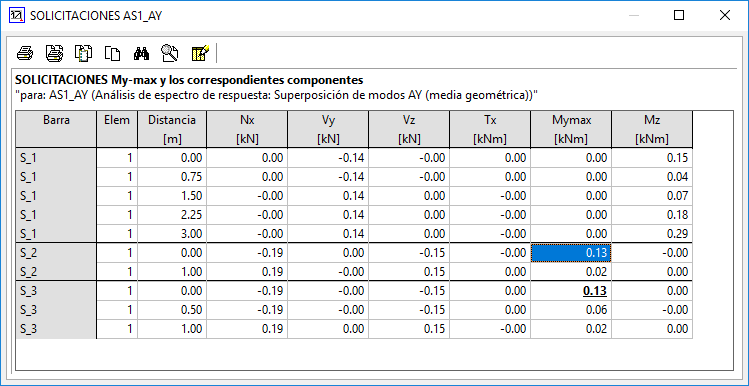
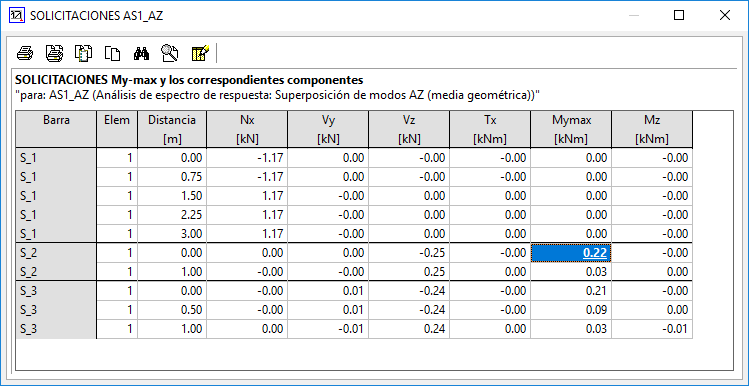
El momento resultado deberá ser My = 0 + 0.13 + 0.22 = 0.35 kNm
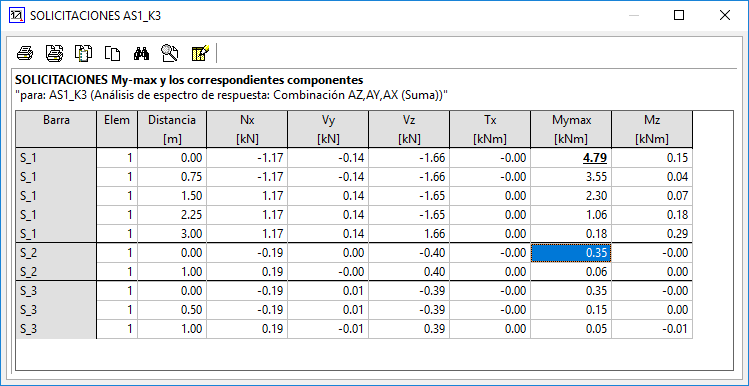
Vemos en la tabla que efectivamente así es.
Método B) SRSS:
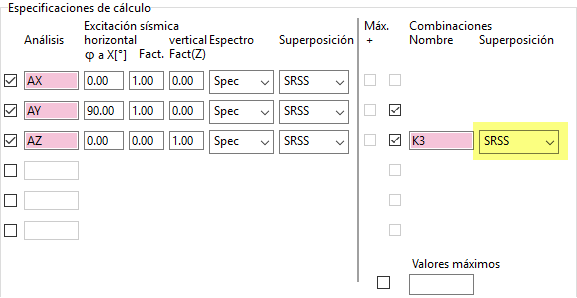
Si seleccionamos ahora el método de combinación SRSS, el momento resultante se obtendría como My = (0^2+0.13^2+0.22^2)^1/2 = 0.25 kNm.
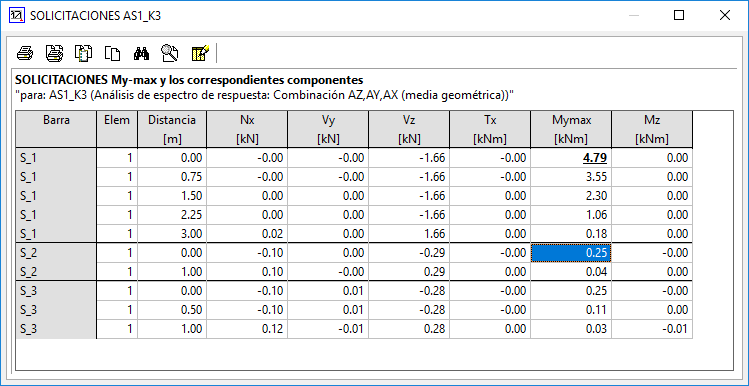
Vemos en la tabla que efectivamente así es.
Método C) Método del Eurocódigo 8.
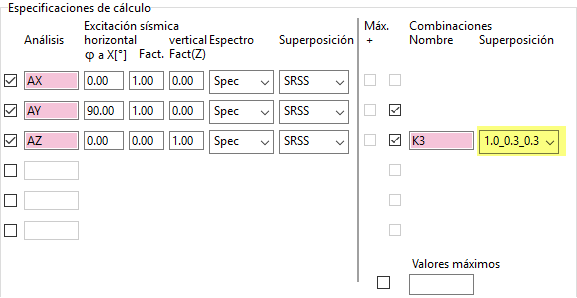
El momento resultante se obtendría como:
My = max (E1, E2, E3) = 0.25 kNm
E1 = 1.0 0+0.3 0.13+0.3 0.22 = 0.11 kNm
E2 = 0.3 0+1.0 0.13+0.3 0.22 = 0.20 kNm
E3 = 0.3 0+0.3 0.13+1.0 *0.22 = 0.25 kNm
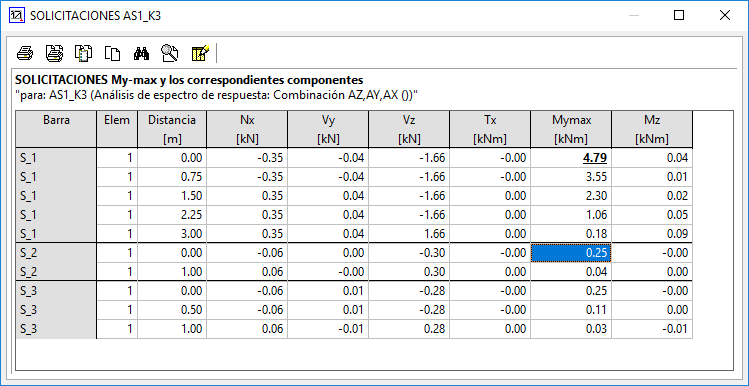
Vemos en la tabla que efectivamente así es.
Para terminar, nos gustaría prestar atención a la opción que aparece en el cuadro de definición del cálculo que destacamos en la siguiente figura:

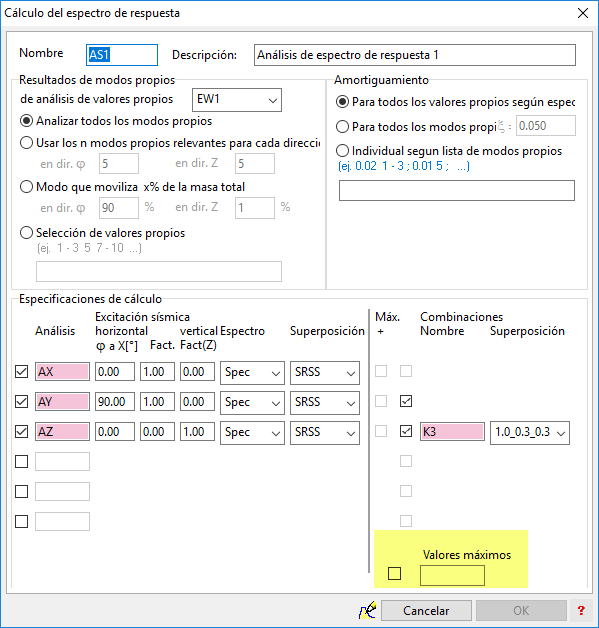
Si marcamos esta opción, el programa comparará los resultados obtenidos para cada una de la especificaciones de cálculo o direcciones de excitación (siempre y cuando marquemos la casilla de la columna "Máx.+" de esa especificación), proporcionando el máximo. Además, es posible compararlo con los resultados de la combinación siempre que se marque (y defina) dicha combinación (por ejemplo, K3) y proporcionará los resultados máximos. Es evidente que, si comparamos los valores obtenidos para las especificaciones con los valores de combinación, siempre serán mayores estos últimos. Por esta razón, STATIK únicamente nos permite emplear los valores de la combinación para el diseño de secciones interactuando con FAGUS. La opción de obtener los valores máximos tendrá utilidad si queremos comparar los valores de las distintas direcciones de excitación entre sí.
Si lo hacemos en nuestro ejemplo:
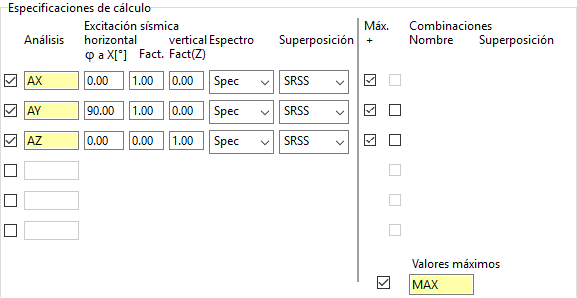
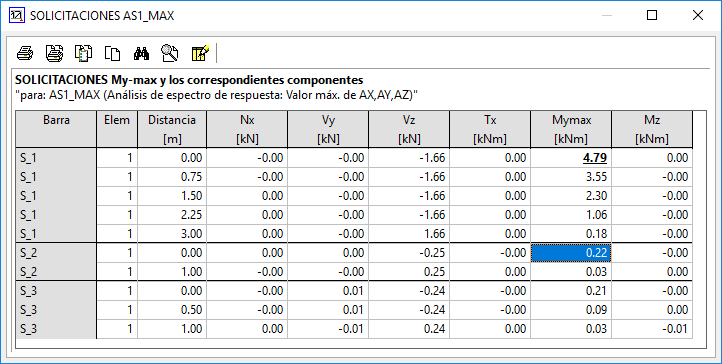
Vemos como el valor de My, por ejemplo para el punto que hemos tomado como referencia, corresponde con el obtenido para la especificación AS1_AZ, por ser el mayor:
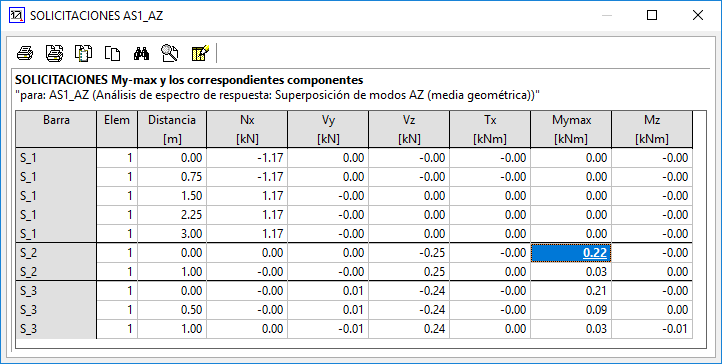
Y también confirmamos lo que decíamos en cuanto a que este valor es menor que el obtenido por combinación (25 kNm), no siendo válido para diseñar.
Este artículo fue originalmente publicado en el Help Center de Cubus-Software España, empresa responsable de la distribución, soporte técnico y formación de los programas Cubus en España, Portugal e Hispanoamérica, y que junto a ingenio.xyz ha desarrollado el único curso online de FAGUS avalado por CUBUS AG (licencia de estudiante disponible).*

Quizás también te interese:


















¿Ya tienes cuenta? Haz login