En esta clase en vídeo del curso de estadística, impartida por Guillermo Castilla, te explicamos las diferencias entre media y mediana de forma muy intuitiva.
Pero antes de empezar, veamos qué representan estas variables estadísticas:
- Media: se trata del centro de probabilidades de una distribución, es decir, el valor que deja la misma probabilidad a ambos lados de la distribución.
- Mediana: se trata del valor central geométrico de la distribución, el valor central del conjunto de datos.
En ciertos casos, la media y la mediana adoptan valores muy similares o incluso idénticos y podemos pensar que esto es extensivo al resto de casos, no entendiendo las diferencias entre una y otra.
La respuesta está en la distribución de los datos.
Los valores de media y mediana son iguales (o muy parecidos) cuando la distribución es simétrica, y es en los casos en los que la distribución no es simétrica en los que la diferencia y la utilidad de cada una de estas dos variables estadísticas se pone de manifiesto.
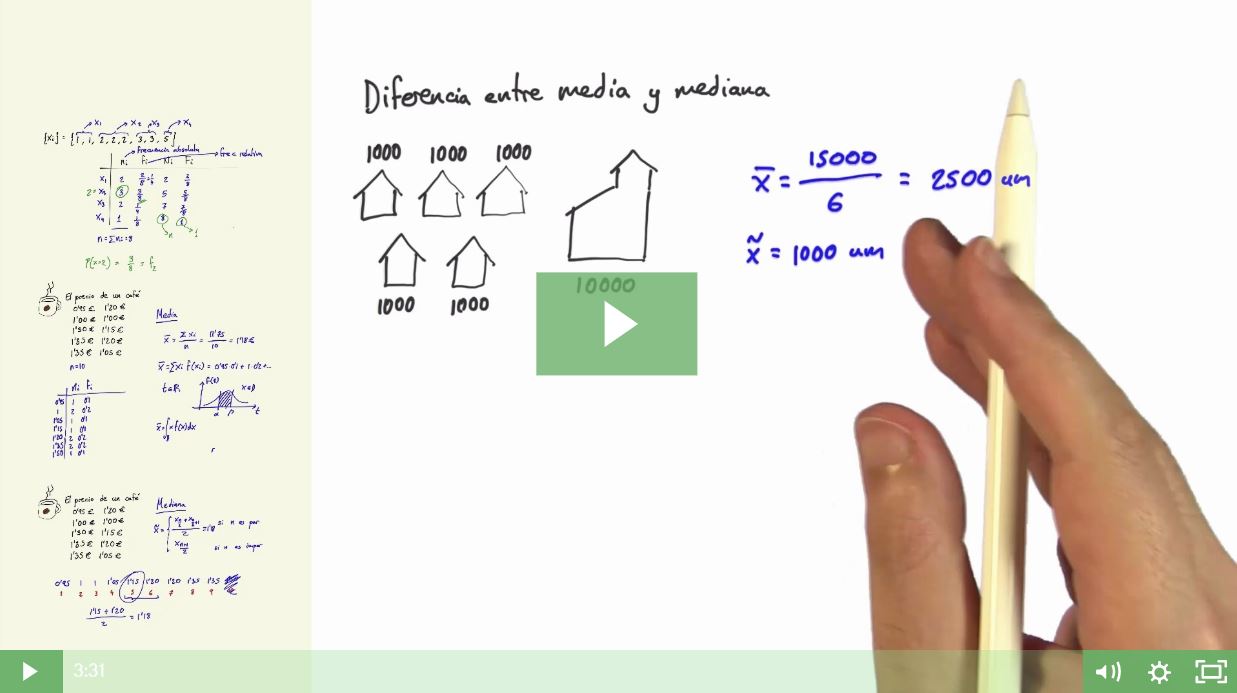
De manera gráfica podemos discernir media de mediana bajo la siguiente premisa: la mediana se va a encontrar justo en el punto medio de una distribución de datos, mientras que la media se va a encontrar en el punto de la distribución que deje a ambos lados la misma probabilidad.
¿Y para qué sirve cada una de estas variables? ¿Por qué se usan?
Estas y otras variables, como la Moda, son útiles para interpretar correctamente el conjunto de datos que estamos analizando, que puede ser muy variable.
En casos en los que la distribución no es simétrica, como el ejemplo inmobiliario que Guillermo plantea en el vídeo, la media estadística no describe la realidad correctamente por sí misma y necesita de otras variables, como la mediana, para lograrlo.
También te puede interesar:
