Para que una estructura pueda permanecer en pie, sin caérsele a nadie encima, ha de cumplir una serie de comprobaciones. Una de ellas es la llamada comprobación de equilibrio, que pese a su nombre, nada tiene que ver con el equilibrio estático de la viga (que significa que las acciones ás las reacciones suman cero).
Para ello Juan Carlos Arroyo nos explica en el curso Números Gordos de Hormigón Armado un pequeño truco muy utilizado en consultorías de estructuras con el que cerciorarnos de que la viga resiste la flexión. Este truco consiste en lo siguiente:
Tomemos una viga con carga uniforme. Esta viga tendrá una ley de momentos flectores elástica. Sin embargo, a veces se quiere armar con leyes parecidas pero no exactas a ésta.
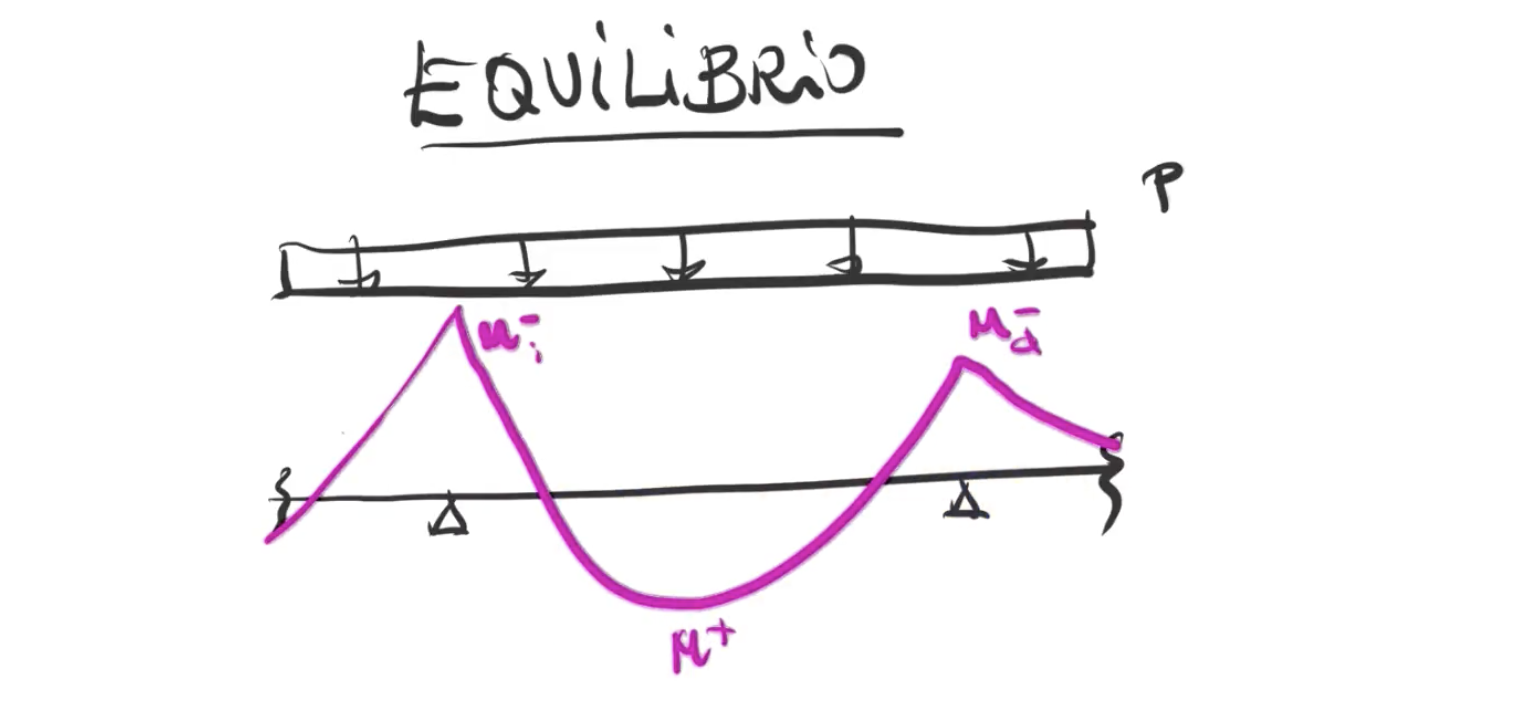
Para verificar si la ley que hemos elegido es adecuada, hay que comprobar si está equilibrada. Para ello comprobaremos que la distancia en el centro de vano entre la línea que une momentos negativos y el momento positivo (la llamaremos ∆M) en un tramo de viga es mayor o igual que Pl²/8. Así de sencillo.
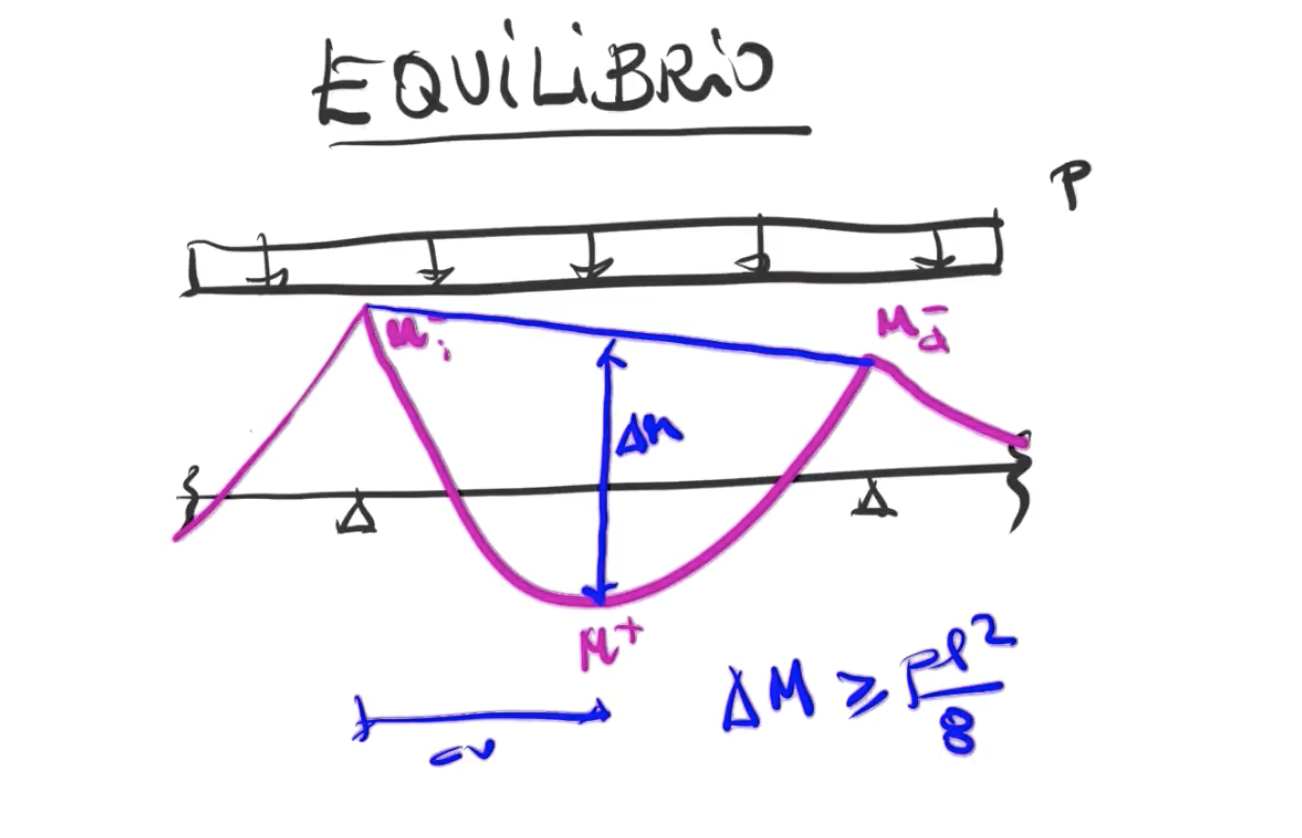
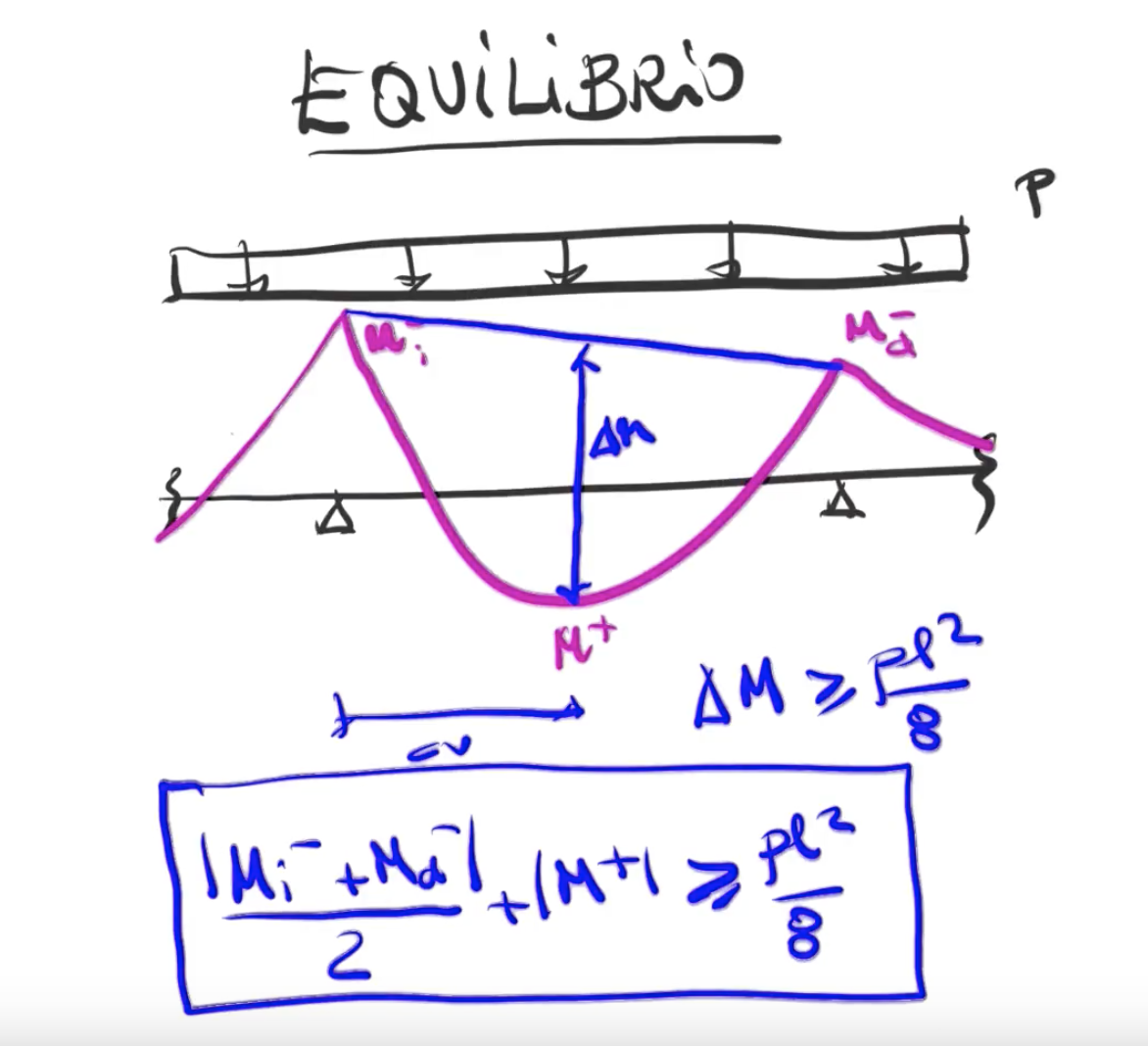
De una forma generalista se podría decir que la semisuma de los momentos negativos y el momento positivo (todo ello en valor absoluto) debe ser mayor o igual que Pl²/8. Esta "herramienta" nos garantiza al menos que dicho tramo de viga no se caerá.
Si eres de los que prefieren el vídeo, aquí te dejamos la clase correspondiente de Juan Carlos en la que habla de esto mismo. ¡Seguro que te queda muchísimo más claro! 😉
También te puede interesar:
Publicado por
