Para calcular y dimensionar secciones en hormigón pretensado debemos conocer tres conceptos específicos de este tipo de estructuras:
- Sección bruta
- Sección neta
- Sección homogeneizada
Veamos con detalle qué son y cómo trabajar con ellas:
Sección bruta
La sección bruta consiste en la sección íntegramente en hormigón, sin tener en cuenta ni la armadura pasiva ni la activa. Por lo tanto, su área será la de la sección rectangular de hormigón, es decir, su base por su altura. La inercia es la correspondiente a la de un rectángulo respecto al centro de gravedad de la sección, estando éste a h/2.
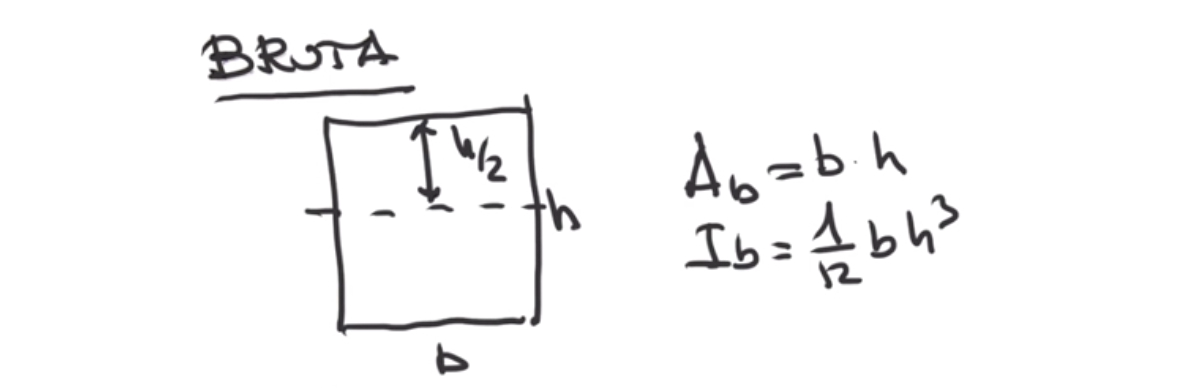
$$ Abruta=b×h $$
$$ Ibruta=1∕12×b×h^3 $$
Sección neta
La sección neta incluye los huecos correspondientes a la armadura pasiva y activa, es decir, cuenta con los espacios vacíos que no suman sección de hormigón, dado que no quedarán rellenos de lechada.
Por lo tanto, el área de la sección neta será el área de la sección bruta restándole las áreas correspondientes a la armadura activa y pasiva.
Para el cálculo de la inercia, el procedimiento ya no será inmediato como en el caso de la bruta, pues tendrá un centro de gravedad diferente de h/2.
Para poder obtener el nuevo centro de gravedad, se toman momentos estáticos respecto de un eje auxiliar, en este ejemplo el superior y se despeja la distancia de este eje al centro de gravedad (Denominado Xneta). De modo que la Xneta será la suma de momentos estáticos dividido entre el área neta.
Una vez obtenido el nuevo centro de gravedad, pasaremos a calcular el momento de inercia neta. Este momento de inercia bruta es igual al momento de inercia de la sección bruta sumado al traslado al nuevo centro de gravedad, y restando los momentos de inercia de los huecos respecto al nuevo centro de gravedad.
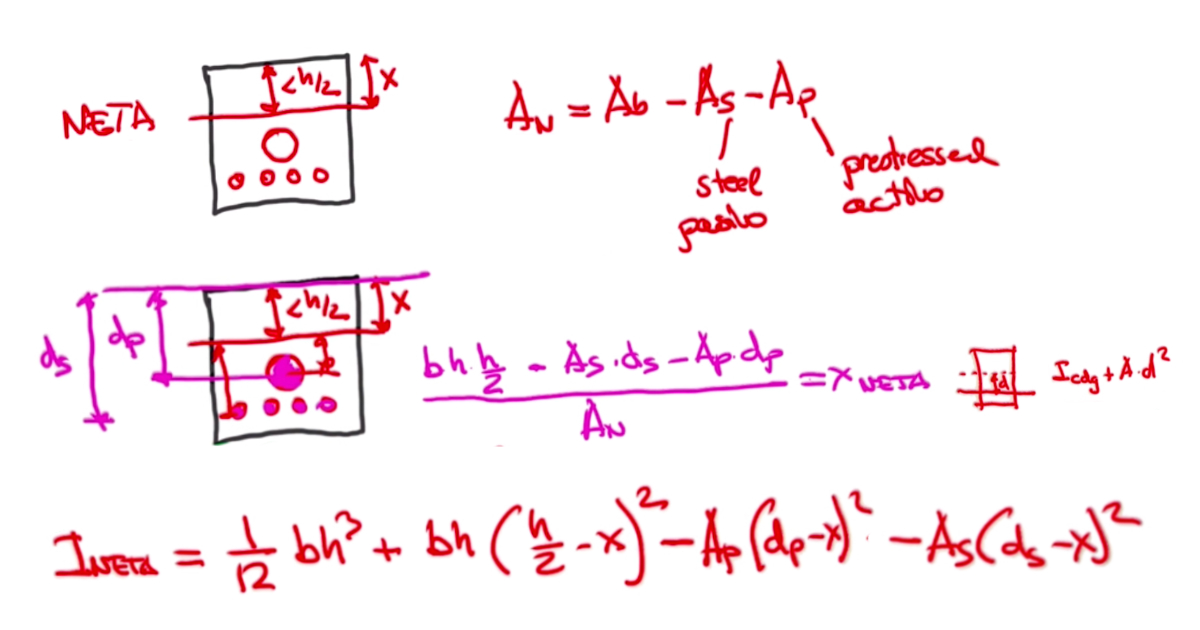
$$ Aneta =Ab-As-Ap $$
$$ Ineta = 1/12×b×h^3 + b×h×(h/2 - x)^2 - Ap×(dp-x)^2 - As×(ds-x)^2 $$
📌 Por tiempo limitado, accede y descarga gratis a una clase relámpago sobre Control de tensiones en hormigón pretensado impartida por Juan Carlos Arroyo. Me interesa.
Sección homogeneizada
Por último tenemos el área más completa, la cual incluye el acero de las armaduras pasiva y activa.
El área homogeneizada será por tanto la suma del área neta, el área de la armadura activa y el área de la armadura pasiva. Ahora bien, debemos prestar atención a esta suma porque estamos operando con áreas de hormigón y armadura, siendo materiales diferentes no podemos realizar la suma de forma directa. A este fenómeno debe su nombre, pues debemos homogeneizar la sección a un único material patrón, habitualmente el hormigón.
Para realizar la equivalencia entre estos dos materiales, trabajaremos con los módulos de deformación, pues es patente que el acero es mucho más rígido que el hormigón. La equivalencia convertirá por tanto el área de acero en un área mucho mayor de hormigon, compensando así la diferencia de rigidez.
Cálculo del área
El acero es n veces más rígido que el hormigón, por lo tanto, el área homogeneizada será el área neta sumando n veces el área de armadura.
En este ejemplo vamos a trabajar solo con armadura activa. Denominaremos al recubrimiento r y al canto útil dp. El hormigón posee un módulo de deformación Ec y el acero Ep
Por lo tanto, el área a la altura de la fibra de la armadura es mucho más rígida que el hormigón luego tendrá más área. El incremento de sección en esta fibra será (n-1)Ap.
Atención, en la equivalencia estamos suponiendo que las fibras de acero y hormigón se deforman lo mismo, luego para realizar el cálculo de tensiones tendremos que deshacer la operación, pues a igualdad de deformaciones, el acero tiene n veces más tensión.
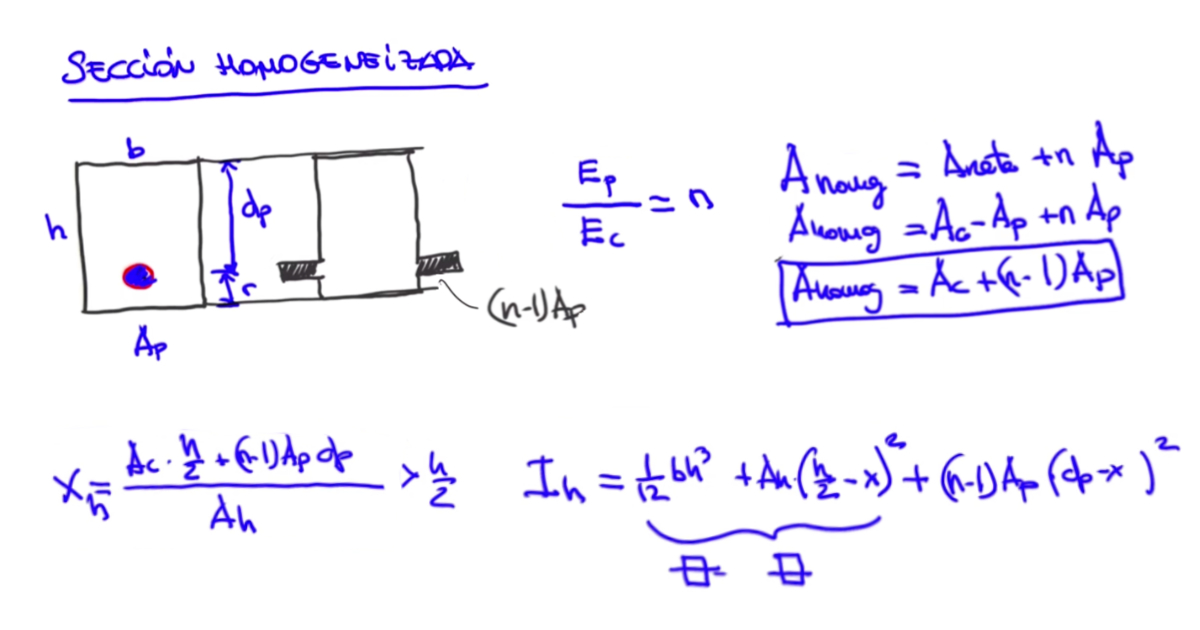
$$ Ahom= Aneta + n×Ap $$
$$ Ahom=Ac+(n-1)×Ap $$
Cálculo de la inercia
Al igual que en el caso de la sección neta, debemos calcular el nuevo centro de gravedad de la sección homogeneizada, encontrándose en este caso por debajo del cdg de la sección bruta.
Los calcularemos de la misma manera, Xhom será igual al cociente de los momentos estáticos respecto de un eje auxiliar entre el área homogeneizada:
$$ Xhom= (Ac×h/2 + (n-1)Ap× dp)/Ahom $$
Por último, calcularemos la inercia de la sección homogeneizada, dividida en tres sumandos.
El primer sumando es la inercia respecto de su eje propio, y el segundo es el traslado mediante steiner de esa inercia a otro eje diferente al que pasa por el centro de gravedad.
Por último, el tercer sumando será el momento de inercia de la armadura respecto al eje que pasa por el centro de gravedad, quedando la expresión tal que así:
$$ Ihom=1/12×b×h^3+Ah×(h/2 - x)^2+(n-1)×Ap×(dp-x)^2 $$
Mejor en vídeo
Te invitamos a echar un vistazo a la clase impartida por Juan Carlos Arroyo, extraída del Curso de Hormigón pretensado. ¡Estamos seguros de que lo entenderás mucho mejor!
¿Quieres formación sobre hormigón pretensado? Consulta todos los detalles del curso de Hormigón pretensado, impartido por Juan Carlos Arroyo, profesor del curso y fundador de Calter Ingeniería, experto en estructuras con más de 30 años de experiencia.
→ Ver más contenidos y cursos sobre Estructuras de hormigón.


















¿Ya tienes cuenta? Haz login