El pandeo es un fenómeno que puede poner en riesgo la estabilidad de las estructuras, por lo que su control es clave para la salud de nuestras edificaciones. Consiste en la aparición de desplazamientos transversales a la dirección de la compresión a lo largo de su longitud. Son especialmente susceptibles de experimentarlo los pilares y el alma de las secciones metálicas. En este post introduciremos el concepto de carga crítica de pandeo y cómo se trabaja con su expresión matemática.
La carga crítica de pandeo es el la máxima carga que es capaz de soportar una pieza conservando su estabilidad. Una vez superado ese valor límite, la pieza sufrirá pandeo a lo largo de su longitud. Para hallarlo, se toma una fórmula obtenida a través de una ecuación diferencial y otras operaciones matemáticas a partir de la teoría de Euler.
$$ Pcr= n^2(π^2×EI)/L^2 $$
Ahora bien, para garantizar la veracidad de la expresión, Euler planteó las siguientes hipótesis a cumplir:
En el traslado de estas hipótesis a la práctica, es intuitivo aceptar que el cumplimiento de estas condiciones es imposible, debido a la imperfección de los sistemas constructivos o de los procesos de fabricación de los materiales.
Si despejamos EI de la fórmula, podemos obtener un valor aproximado de la rigidez a flexión necesaria para una determinada carga de pandeo, lo que nos puede ser muy útil de cara a predimensionar la estructura. No obstante, debemos prestar atención al margen de seguridad que aplicamos, pues se debe recordar la imposibilidad de llevar a la práctica las hipótesis de la teoría de Euler que verifican la expresión.
Partiendo de una columna biapoyada sometida a una carga P, en su extremo inferior aparecerá la correspondiente reacción de igual valor. Cuando la carga P alcance el valor de la carga crítica de pandeo Pcri, se producirá la inestabilidad. En el ejemplo típico de pilar biapoyado , la morfología de pandeo será muy intuitiva, siguiendo el modelo de n=1.
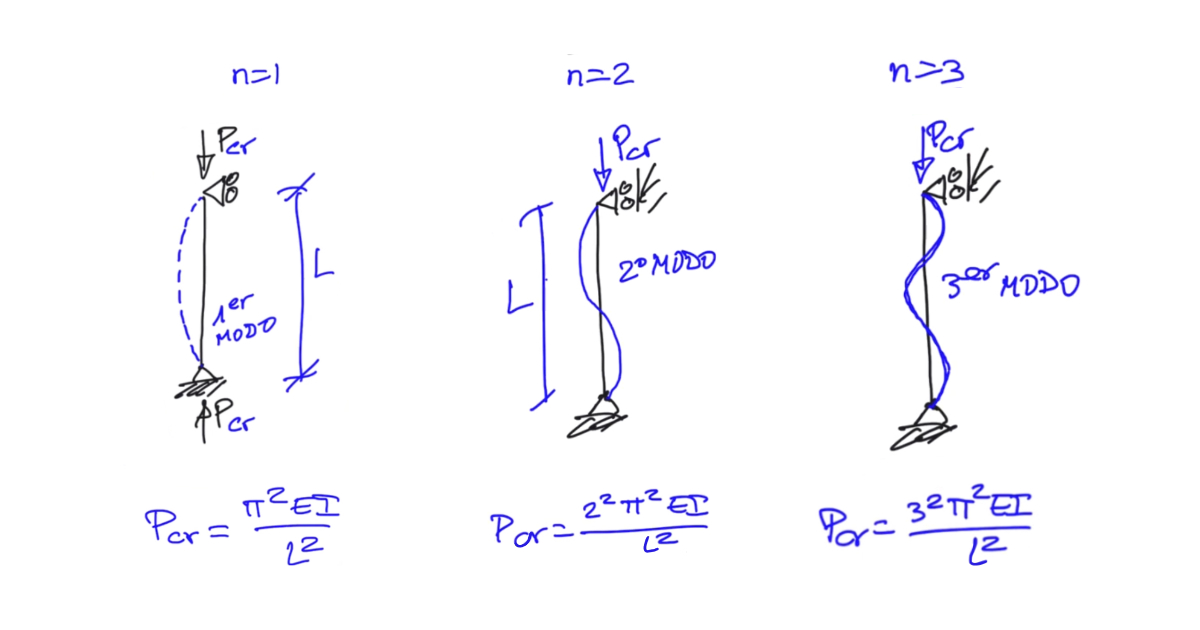
La teoría de Euler formuló modos de pandeo teóricos para diferentes valores del valor n; cambiando la morfología del pandeo y el valor de su carga crítica. Estos modelos obtienen cargas críticas de pandeo cada vez mayores; por lo tanto, en la aplicación a estructuras reales, el modo de pandeo que seguirá el elemento será el obtenido para una menor carga crítica, generalmente el n=1. No obstante, existen configuraciones estructurales que son susceptibles de pandear de estos modos alternativos, como pilares confinados en puntos a lo largo de su longitud.
En Ingenio.xyz creemos que el aprendizaje es más efectivo cuando te lo explican los mejores profesionales. Echa un vistazo a la clase extraída del curso de Pandeo e inestabilidad de estructuras, impartida por Juan Carlos Mosquera.
¿Quieres conocer a fondo el fenómeno del pandeo? Consulta todos los detalles del curso de Pandeo e inestabilidad de estructuras, impartido por Juan Carlos Mosquera, profesor del curso y autor de diversas publicaciones sobre cálculo de estructuras como el libro "Resistencia de materiales"
Las comunidades de ingenio.xyz te conectan con los máximos expertos en la materia. Preguntas y respuestas, materiales extra en torno a los cursos y recomendación de recursos.
Accede a recursos exclusivos, el area de preguntas y respuestas y descuentos exclusivos para miembros en los cursos de ingenio.xyz.
¿Ya eres miembro? Haz login.
¿Crees que ingenio.xyz puede interesar a tus colegas de profesión? Coméntaselo.
Haz login o regístrate para comentar.