Cálculo de tensiones normales y tangenciales

El comportamiento de las estructuras metálicas viene dado por las características mecánicas y geométricas de sus secciones. Es por ello que resulta tan importante manejar con soltura la distribución y cálculo de los estados tensionales de estos elementos. En este post se tratará el cálculo general de tensiones normales y tangenciales.

Cálculo general de tensiones normales.

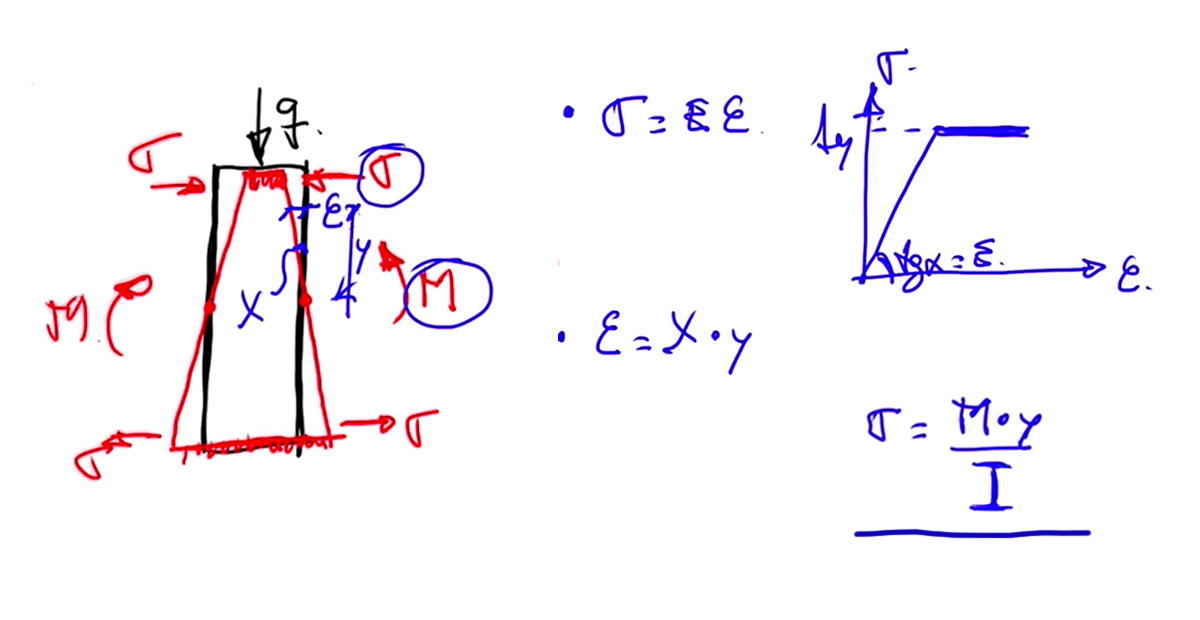
Para introducir el cálculo de las tensiones normales, vamos a profundizar sobre cómo es la deformación de la sección vertical de una pieza metálica por efecto de las cargas. Las caras de la rebanada que son planas previo sometimiento a la carga, lo serán también después de introducirla. Por lo tanto, el efecto de la carga se evidencia en el giro de estas caras. A raíz de la aparición de las tensiones normales, la parte superior de las rebanadas se comprime, acortándose; y la inferior se tracciona, alargándose. La integral de las tensiones normales resultantes es el momento flector. Debemos hallar la relación existente entre la tensión normal σ y el momento flector M. Para realizarlo nos apoyaremos en dos conceptos:

• El régimen elástico, en el cuál las tensiones son proporcionales a las deformaciones. El acero se encuentra en este régimen para valores tensionales razonables. Su módulo elástico es precisamente la constante de proporcionalidad entre tensión y deformación; siendo válido hasta alcanzar un valor llamado límite elástico, a partir del cual se pierde tal característica.
• Hipótesis de la deformación plana. La deformación en un punto cualquiera de la rebanada, es decir, la distancia del punto original sin deformación, al punto una vez deformada, es proporcional a la distancia del punto al eje de giro, pasando este eje por el centro de gravedad.
  • ξ=χ·y siendo: ξ: deformación, χ: giro de la rebanada, y: distancia del punto al eje.

Relacionando ambas condiciones obtenemos la siguiente expresión:

$$ σ = (M · y)/I $$

Siendo:

σ : Tensión normal M : Momento flector

y: Distancia del punto elegido al eje de giro.

I : Inercia de la sección resistente.

Cálculo general de tensiones tangenciales.

Al igual que se ha obtenido la tensión normal en un punto de la sección, se invertirá el proceso para obtener la tensión tangencial. La integral de la tensión tangencial es el cortante. Dada esa resultante, se busca obtener la tensión tangencial en cualquier punto de la sección. Para ello, volvemos a utilizar las expresiones anteriores:

• Régimen elástico.
• Hipótesis de deformación plana.

A partir de ambas, obtenemos la relación, con la salvedad de que la expresión resulta:

τ=G·γ , siendo: τ : tensión tangencial, G: módulo de elasticidad transversal, γ: deformación angular por efecto de las tensiones tangenciales.

Por lo tanto, la expresión final para el cálculo de las tensiones tangenciales es:

$$ τ=Q·Sx/I · t $$

Siendo:

τ: Tensión tangencial

Q: Cortante

Sx: Momento estático

I: Inercia

t: Espesor de la pieza.

Condicionantes geométricos

Ahora bien, para que estas formulaciones y relaciones sean válidas, más allá de estar en régimen elástico se debe cumplir una condición más:

• La sección debe ser abierta y de pared delgada.

De modo que esta fórmula no podrá ser usada para secciones llenas o rectangulares. De forma general, esta restricción no debe preocuparnos, pues la gran mayoría de estructuras metálicas las cumplen, ya sean perfiles en C, en U o doble T. Sólo la excluiremos del cálculo en perfiles cerrados como los de sección cuadrada.

Te lo explicamos en vídeo

En Ingenio.xyz creemos que el aprendizaje es más efectivo cuando te lo explican los mejores profesionales. Echa un vistazo a la clase extraída del curso de Estructuras metálicas: fundamentos, impartida por José M. Simón-Talero.

¿Quieres dominar el cálculo de secciones metálicas? Consulta todos los detalles del curso de Estructuras metálicas: fundamentos, impartido por José M. Simón-Talero, actual CEO de Torroja Ingeniería y profesor de estructuras metálicas en la E.T.S.I. Caminos, Canales y Puertos.

→ Ver más contenidos y cursos sobre Cálculo de estructuras.