Cuando un elemento estructural esbelto se ve sometido a compresión, pueden aparecer desplazamientos transversales a la dirección de la compresión a lo largo de su longitud. Este fenómeno se denomina pandeo y son especialmente susceptibles de experimentarlo los pilares y el alma de las secciones metálicas. En este post resolveremos un ejemplo sencillo sobre cómo plantear y resolver un problema de pandeo lateral en una pieza bi-apoyada recta de madera. ¡Vamos a verlo!
Planteamiento
Partimos de una pieza de madera recta en toda su longitud y de sección constante. Sus dimensiones son l=2 m de largo por b=0,1 m de ancho y h=0,25 m de canto. Su módulo de elasticidad es E=10 GPa. Está apoyada en sus extremos, teniendo un apoyo fijo y otro deslizante. Se somete al elemento a una carga puntual axial de valor P de compresión sobre el apoyo deslizante.
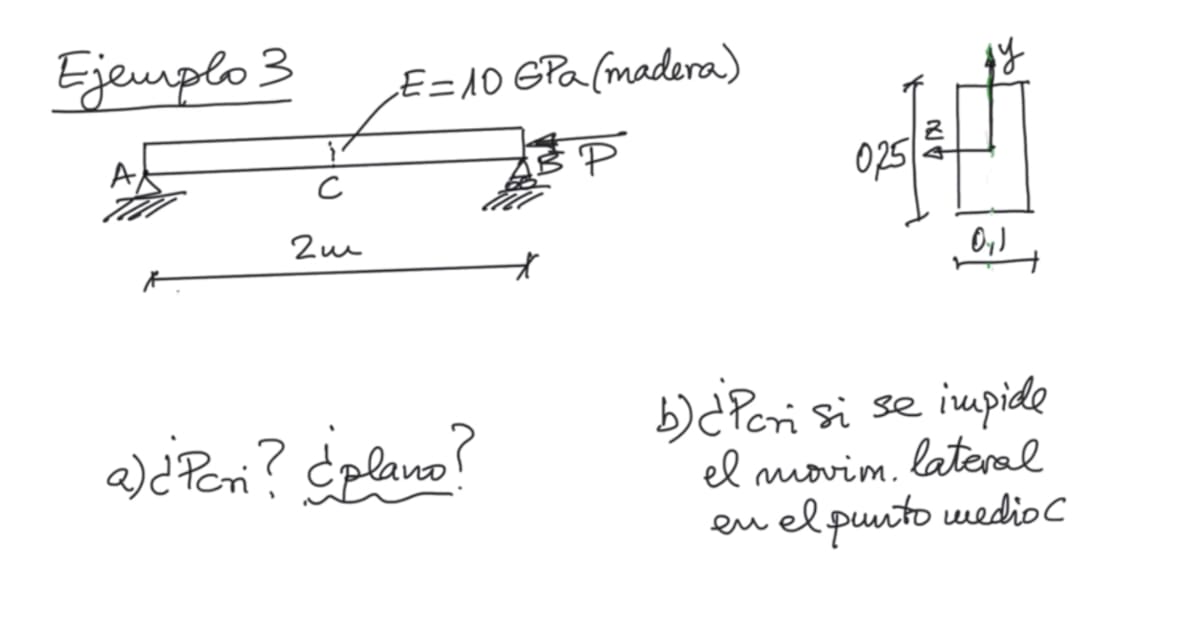
Las cuestiones a resolver son:
- ¿Qué valor deberá tomar la carga para que se produzca pandeo en la pieza? ¿En qué plano se experimentará el pandeo?
- Si en el punto medio de la pieza se impidiese el movimiento lateral con el fin de evitar el pandeo de la pieza fuerza de su plano, ¿Cuál sería la carga de pandeo? ¿En qué plano se experimentaría el pandeo?
Primera parte: Carga de pandeo sin confinamiento de la pieza
Como punto de partida, vamos a imaginar un sencillo ejemplo para entender mejor el pandeo. Si tomamos una regla escolar y la comprimimos con las manos, la regla pandeará lateralmente. Es intuitivo pensar que lo hará en el eje en el que posee un canto muy pequeño. Luego el desplazamiento se experimentará en la dirección en la que el elemento posee menor momento de inercia.
En la fórmula del momento de inercia en una sección rectangular respecto del eje que pasa por el centro de gravedad, la altura de la sección se encuentra al cubo. Por lo tanto, el valor del canto es el que tiene una mayor trascendencia. Teniendo esto en cuenta, en el caso de la regla y en el problema planteado, el pandeo se producirá en el eje de menor momento de inercia, el de menor canto.
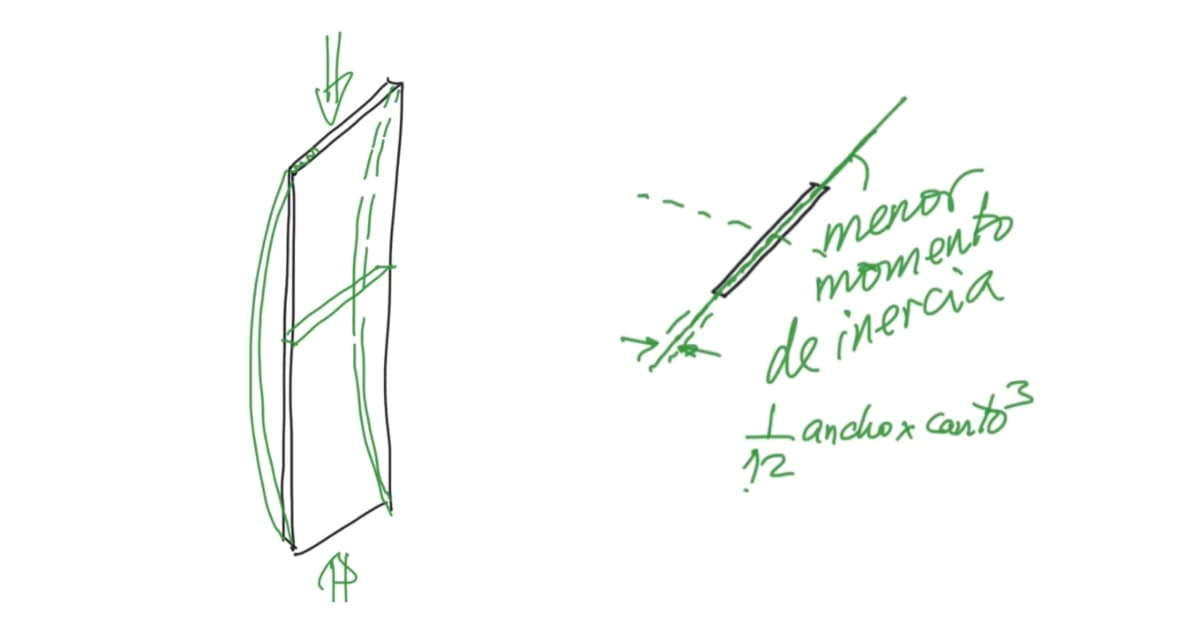
Momento de inercia de una sección rectangular
$$ I=1/12×b×h^3 $$
Procedemos a calcular este momento de inercia para la sección dada: I=2083,333 cm4. Ahora, calcularemos el valor de E×I, prestando especial atención a ser coherentes con las unidades, cambiando los valores a kilonewtons y a metros, de modo que resultará E×I = 208,333 KNm^2. El eje de flexión para el pandeo es el plano débil, por consiguiente, se producirá pandeo fuera del plano de la pantalla.
Por último, para calcular la carga crítica de pandeo, utilizaremos la fórmula de EULER. Para hallarla debemos introducir el concepto de longitud de pandeo, que depende de la longitud real y del coeficiente λ, dado por la situación de la pieza. En este caso, al ser biapoyada λ=1 y la longitud real es igual a l=2m , luego Lp=1×2=2m.
Longitud de pandeo
$$ Lp=λ×l $$
Obtenidos los valores de E×I y Lp, tenemos todo lo necesario para hallar la carga crítica de pandeo, que resultará Pcri=513,54 KN.
Carga crítica de pandeo de EULER
$$ Pcri=(π^2×E×I)/Lp^2 $$
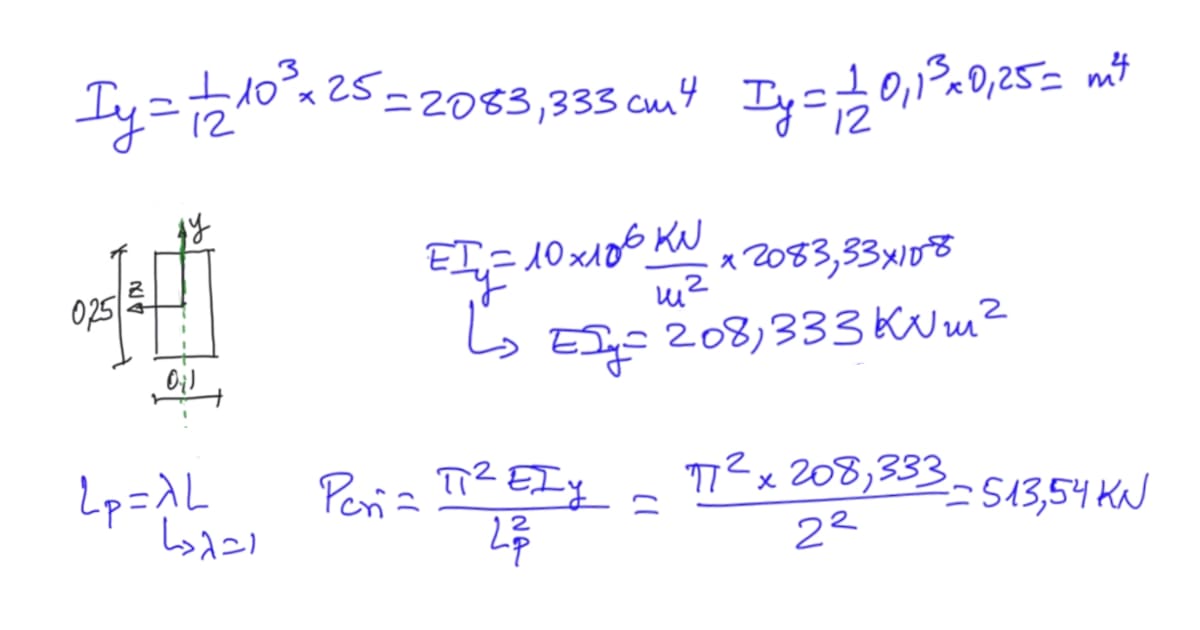
Segunda parte: Carga de pandeo con confinamiento de la pieza
Con el fin de que la viga no se deforme fuera del plano de la pantalla, se procede a someter su punto medio a un confinamiento. Así pues, puede producirse pandeo en los dos segmentos resultantes, pero no así en su punto medio. Se debe estudiar la posibilidad de pandeo en los tramos CA y CB.
Hipótesis 1
La primera situación a estimar es la experimentación de pandeo respecto del eje Y, al igual que en el caso anterior, pero variando su longitud de pandeo debido al confinamiento.
Por lo tanto, para el pandeo de uno de los tramos se utilizará la misma rigidez asociada a flexión que en el caso anterior E×Iy=208,333 KNm^2. Luego en la fórmula del pandeo sólo variará el valor de la longitud de pandeo Lp=1m, resultando la carga crítica de pandeo Pcri=2054,16 KN. Podemos resaltar cómo este valor es exactamente 4 veces el dado sin confinamiento del punto C.
Hipótesis 2
La segunda hipótesis será la del pandeo en el eje Z, es decir, hacia arriba o hacia abajo en el plano de la propia figura. Como primer paso, calcularemos la inercia respecto del eje Z de la sección: Iz= 1302,0833 cm4. Ahora lo multiplicamos por el módulo de elasticidad y realizamos la conversión de las unidades, quedando tal que EI= 1302,0833 KNm^2. Por último, hallamos la carga crítica de pandeo con Lp=2m, siendo por tanto Pcri=3209,64 KN.
Conclusión
El análisis de ambas situaciones nos muestra que la pieza puede pandear en sus segmentos menores en el plano fuera de la pantalla, pues su carga de pandeo es menor que la carga de pandeo propia del plano vertical.

Te lo explicamos en vídeo
En Ingenio.xyz creemos que el aprendizaje es más efectivo cuando te lo explican los mejores profesionales. Echa un vistazo a la clase extraída del curso de Pandeo e inestabilidad de estructuras, impartida por Juan Carlos Mosquera.
¿Quieres conocer a fondo el fenómeno del pandeo? Consulta todos los detalles del curso de Pandeo e inestabilidad de estructuras, impartido por Juan Carlos Mosquera, profesor del curso y autor de diversas publicaciones sobre cálculo de estructuras como el libro "Resistencia de materiales"


















¿Ya tienes cuenta? Haz login