Buenos dias,
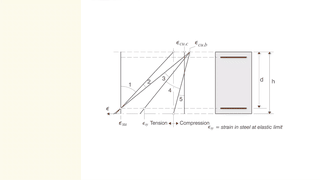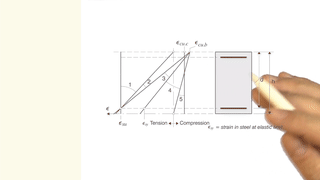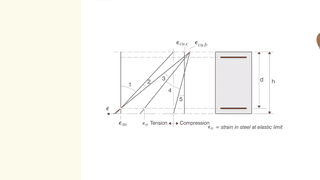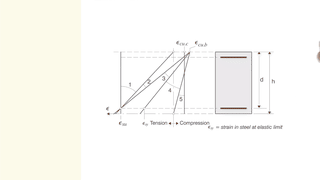
en relacion al planos de rotura, come se puede specificar en Fagus que despues el puento C, el plano no es lineal? Esto porque tiene una linea recta dal puento B al puento C y despues el plano gira en torno el puento C. Yo estoy hacendo referencia al caso cuando tiene una compression muy elevada y l'eje neutral es fuera de la seccion.
Muchas gracias,
Edoardo