Buenas,
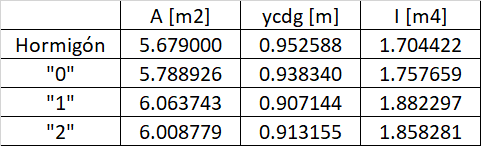
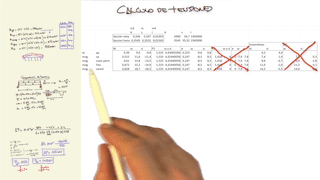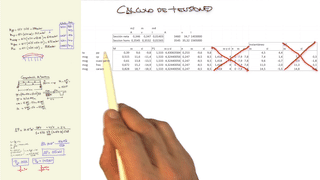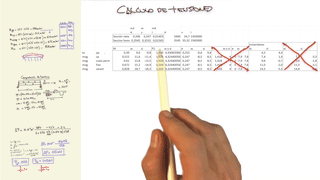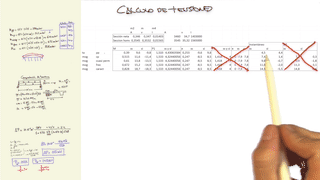
Para calcular las tensiones a tiempo infinito se están teniendo en cuenta las pérdidas diferidas. Sin embargo, se opera con las características de la sección homogeneizada a tiempo cero. Para ser estrictos, habría que operar con la sección homogeneizada a tiempo infinito, ¿no? En este caso, el área y la inercia aumentan al "rigidizarse el acero respecto al hormigón" (al aumentar el coeficiente de equivalencia por la disminución virtual del módulo de elasticidad del hormigón con el coeficiente de fluencia).
Un saludo.