Hola,
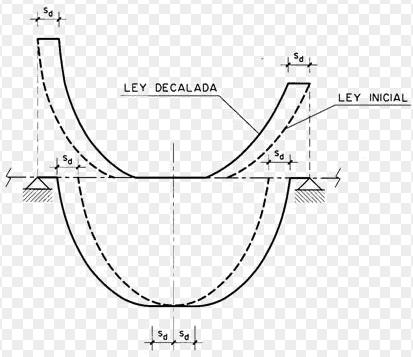
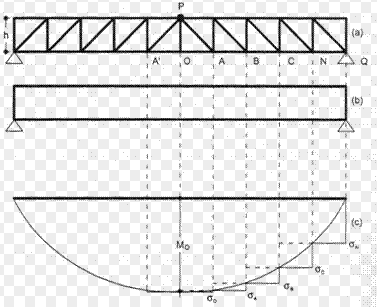
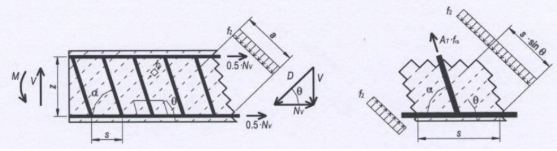
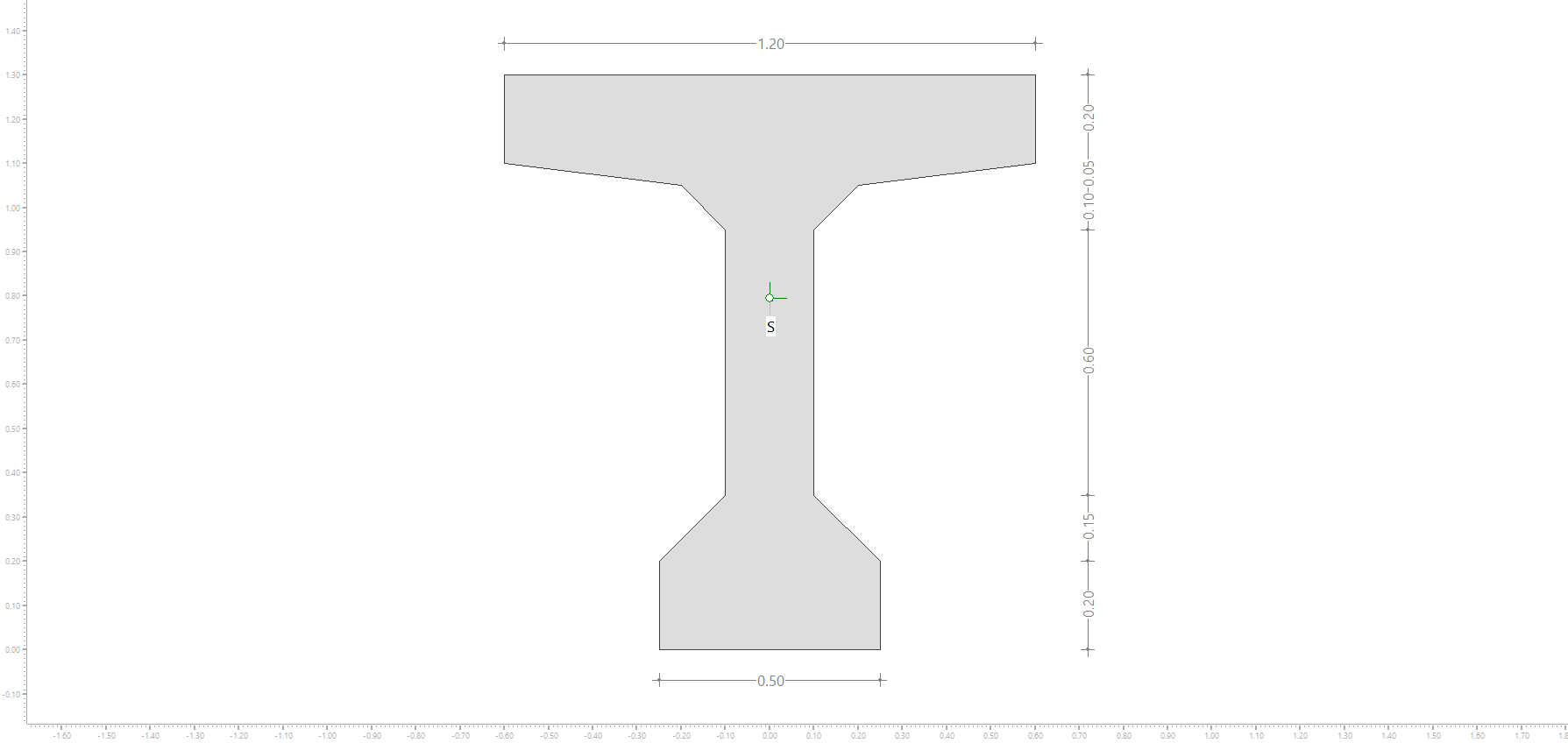
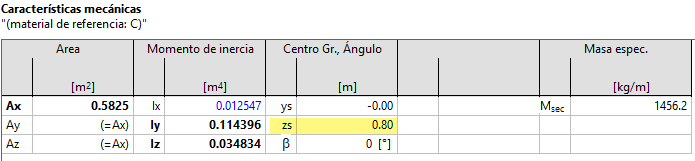
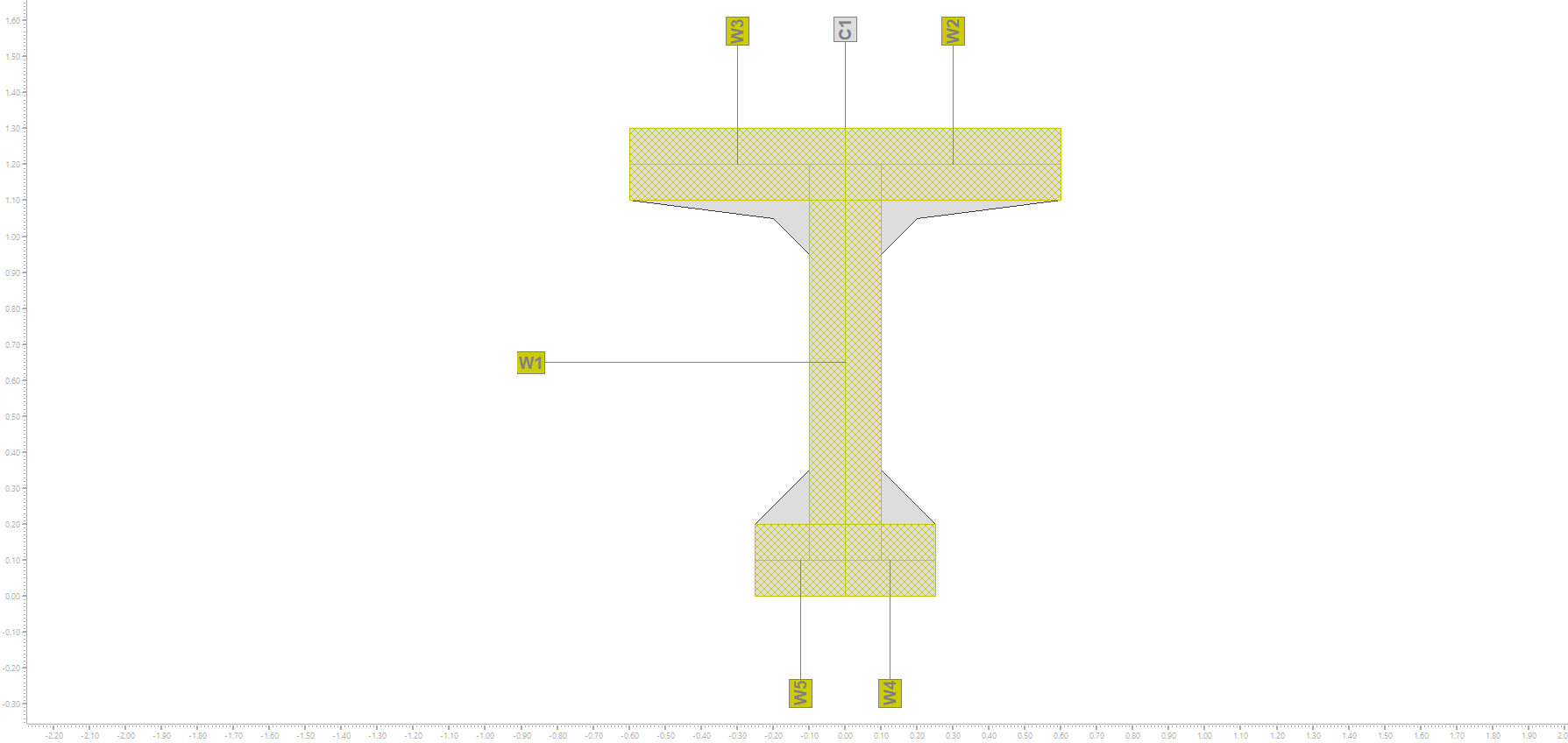
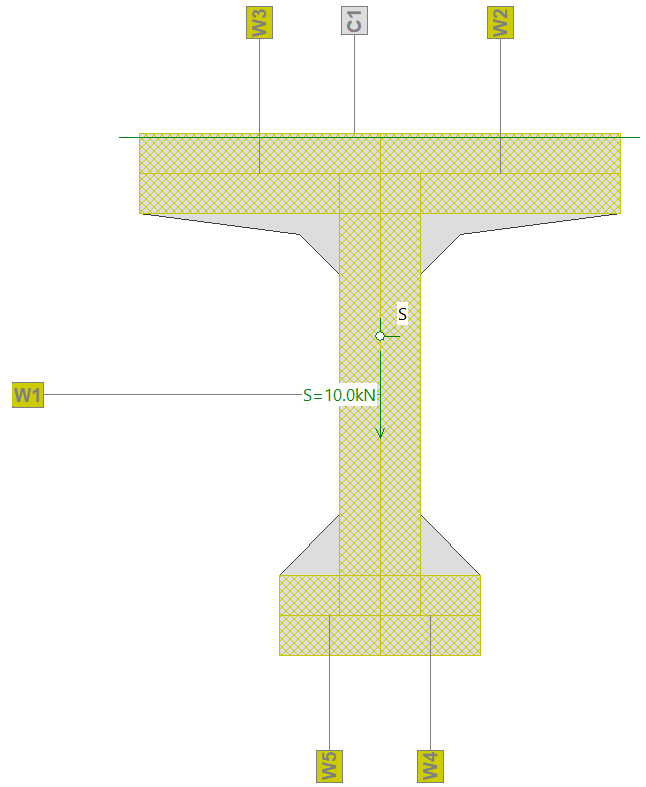
yo è entendido que la fuerza longitudinal debida al cortante es 9 kN (porque l'incinacion es 45°). Esta fuerza es localizada en la armadura longitudinal que tiene una ecentricidad con respecto de el cientro de gravidad de la seccion. En la transformacio que Fagus hace por My, el tiene en cuenta que la fuerza de 80 kN es aplicada en el axis point. Porquè la ecentricidad de la fuerza longitudinal debida al cortante no se toma en cuenta en la trasformacion de My?
Muchas gracias,
Edoardo