Dudas en el control de la fisuración por contracción térmica inicial en muros

Hola José Alonso,

La duda que planteas es recurrente, y yo creo que es debido a que la tabla que refieres de la EHE no es del todo correcta, o mejor dicho, quizás sea excesivamente simplificada.

Efectivamente, si consideramos los acortamientos por temperatura y retracción coartados en la base de los muros (coacción que se producirá porque la cimentación ya habrá retraído en gran medida y se opondrá al acortamiento del alzado del muro) las tracciones originadas por dicha coacción no dependen de la longitud y, por tanto, el emplear juntas de contracción -por ejemplo a 7,5 m como sugiere la EHE- no permitiría reducir la cuantía de fisuración. Según este planteamiento y de forma simplificada, todo muro, independientemente de su longitud, debería calcularse a tracción, y en función de la abertura de fisura que se admita, el salto térmico (contracción térmica inicial y variación estacional) y la retracción hidráulica, calcularse la cuantía de armadura necesaria.

En los casos habituales, dicho cálculo arroja cuantías entre el 0,35% y 0,45 %, coherentes con el 0,40 % de la tabla de la EHE. Sin embargo, en nuestra opinión, al menos en el tramo inferior del muro (en torno a 0,2L, siendo L la distancia entre juntas como verás más adelante), dicha cuantía no debería disminuirse por el hecho de disponerse juntas.

A partir de dicha altura la coacción al acortamiento que induce el cimiento es menor, y por ejemplo el Eurocódigo permite tener en cuenta un coeficiente reductor de la coacción mediante un coeficiente R:

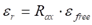
Dicho coeficiente también tiene en cuenta la relajación de las tensiones de tracción por efecto de la fluencia (coeficiente K, normalmente se considera 0,5). Además, al producirse la fisura no se liberan totalmente las tracciones en el hormigón (que simplificadamente se puede tener en cuenta considerando una contracción “reducida”

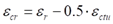
, siendo el último término la deformación a tracción del hormigón para el que éste se fisura -así lo hace el CIRI 660, documento para aplicación de los eurocódigos en el Reino Unido), el cálculo de la cuantía de armadura se puede realizar con la siguiente expresión:

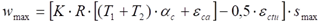
En la figura y tabla siguientes te copio el coeficiente reductor (Rax =K·R) que recoge el Eurocódigo UNE EN 1992-3 (Depósitos y estructuras de contención). Como ves, cuando la coacción es total (por ejemplo en la base), R=1 y K=0,5, por lo que K·R=0,5):

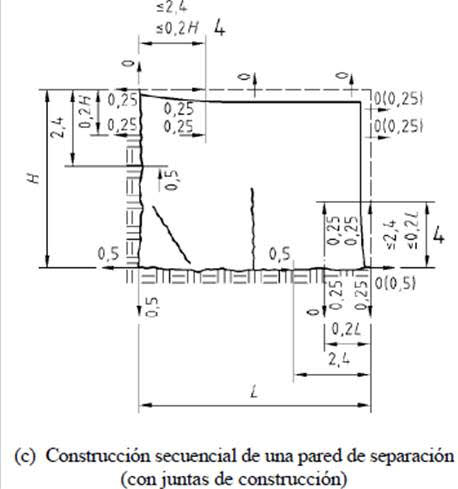
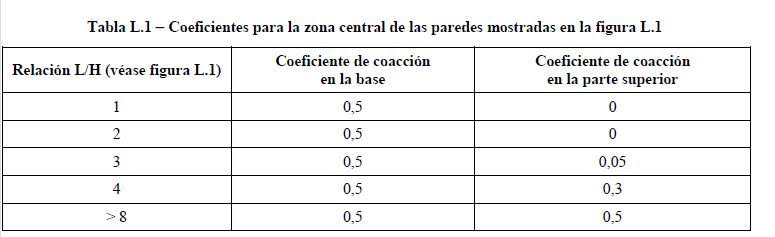
Como deduces de esta tabla, la reducción de la coacción en el tramo superior del muro no depende lógicamente de la distancia entre juntas, sino de la relación L/H (si la distancia entre juntas es 7,5 m, pero la altura del muro es de 1 m, la reducción sería mínima).

Así por ejemplo, para un muro de 3,75 m de altura y distancia entre juntas 7,5 m, los 1,5 m inferiores habría que armarlos con una cuantía horizontal del orden del 0,4 % (esta estimación puede variar en función de si se hormigona en verano o invierno, la abertura de fisura que se admita, el cemento empleado, el recubrimiento y diámetro de la armadura horizontal -determinantes en el cálculo de la abertura de fisura- etc.), y el resto, con la mitad de cuantía.

Espero haber contestado a tu consulta.

Un saludo.

Muchas gracias Eduardo Diaz-Pavón por vuestra explicación, ha despejado totalmente las dudas relativas a la influencia de la longitud del muro en la contracción térmica inicial de muros.
No obstante, para terminar de aclarar la información facilitada, la cuantía horizontal del orden del 0,4% que al final se especifica ¿se repartiría en las dos caras del muro en ese 1,5m que se plantea en el ejemplo? ¿cómo influye en este tipo de fisuración no sólo cuanto cemento se emplee sino el tipo de cemento utilizado? Para controlar esta fisuración querría confirmar si interesa mayor número de barras de menor diámetro que pocas de mayor diámetro.
Un saludo

Si, esa cuantía es a repartir en las dos caras.
Én cuanto a la dosificación, como en todos los fenómenos higrotérmicos del hormígón, es determinante. Si el cemento es normal (tipo I) y su contenido elevado, el calor de hidratación también será mayor y el riesgo de fisuración a edades tempranas igualmente mayor.
Por último, para controlar la fisuración siempre conviene más barras de menor diámetro con el menor recubrimiento posible.
Saludos.