T no igual a C/Comprobacion de secciones

Hemos dicho que la compresión y la tracción deben ser iguales para que haya equilibrio en la sección ya que no hay axiles Como la relación tensión-deformación en el acero es una línea horizontal a partir de fyd, implica que la fuerza de tracción permanece constante entre la deformación de fyd y la deformación ultima. Sin embargo, la fuerza de compresión va aumentando al bajar la línea neutra para la misma tracción. Por tanto no habría equilibrio de fuerzas horizontales. Imagino que ello se engloba dentro de las simplificaciones y que realizamos, ya que los diagramas no son realmente horizontales. Voy bien?
Supongo que por ello cuando calculamos el Mlimite utilizamos la compresión en lugar de la tracción y obtenemos una fórmula que solo depende del hormigón
Ahora bien, lo que busco ahora es hacer el camino a la inversa, es decir, comprobar una sección que tiene una armadura determinada y quiero hallar el M que soporta. Quería saber si podría hacerlo de la manera siguiente:
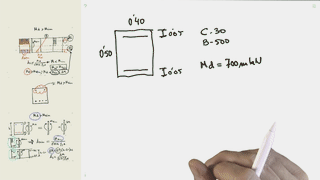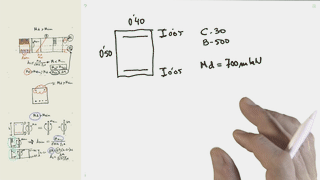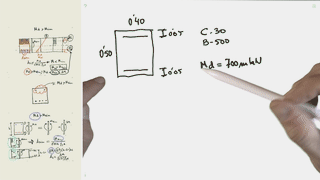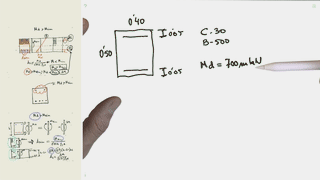
Tendría que hallar la Z exacta. Para ello impondría la max. Deformación del hormigón y la deformación el 2,17% del acero. Por semejanza de triángulos hallaría la Z que multiplicada por el As que conozco y por fyd sería el momento máximo que soporta la tensión. En este caso considero que toda la armadura de tracción equilibra a las tensiones del hormigón.
Pero como la sección tendrá una armadura de montaje superior, podría considerar su aportación en compresión. Restaría de la armadura de tracción el área de la armadura de compresión. Realizar el cálculo anterior y luego sumarle el momento que soporta la sección debido a la armadura superior. Así obtendría un valor de M último mucho más preciso. Que te parece?