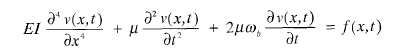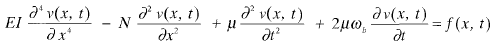Análisis dinámico viga pretensada

Question

Hola a todos,Me surge una duda con respecto al comportamiento dinámico de una viga de hormigón. Si consideramos dicha viga como un elemento de hormigón armado, obtendremos unas frecuencias propias de vibración para esa viga.Si ahora introducimos una fuerza de pretensado, mi intuición me dice que la rigidez de la viga variará, y en consecuencia sus frecuencias propias de vibración. ¿Estoy en lo cierto, o el comportamiento dinámico no depende de la fuerza de pretensado?, o en otras palabras, dos vigas, una de hormigón armado y la otra de hormigón pretensado, de la misma longitud, misma sección transversal y mismo material ¿tendrán las mismas frecuencias?En este razonamiento no he tenido en cuenta la variación de inercia de la viga en un caso y otro por homogeinización de la sección, me interesa conocer si la fuerza axial que introduce el pretensado modifica el comportamiento dinámico. ¿qué opináis?Muchas gracias.Un saludo,Manuel Aguilar.

Juan Carlos Arroyo · Accepted Answer

Hola Manuel:

Una viga de hormigón armado fisura bajo las acciones de servicio (si no fisura, te estás gastando demasiada pasta ;) ).

En una viga de hormigón pretensado puede haber dos situaciones:
A) Que no fisure bajo la acción de la sobrecarga, en cuyo caso la rigidez es siempre la bruta
B) Que fisure bajo la acción de la sobrecarga, en cuyo caso la rigidez es menor. Sin embargo, por haber una compresión, puede garantizarse que la fibra neutra esta´r más baja y también, aunque en menor medida, la inercia es mayor que la d la viga fisurada sin compresión

La realidad es que la viga postesada es más rígida que la armada:
- Una cantidad importante, 2 ó 3 veces, si se ha proyectado en el caso A
- Una cantidad poco relevante si se ha proyectado en el caso B

Los cálculos, claro, dependen de lo que consideres. Si haces los cálculos de la frecuencia con hormigón armado pero secciones brutas, la diferencia de resultados es poca ;)
Ojo, que los cálculos dinámicos con rigideces fisuradas, fáciles no son. Salvo que apliques fórmulas simplificadas.

Un saludo cordial

Manuel Aguilar García · Answer

Muchas gracias por la respuesta Juan Carlos.

Para aclarar un poco más el concepto, suponiendo que ahora las dos vigas son pretensadas y que todas las fibras de su sección están comprimidas, ¿las frecuencias propias de vibración deberían variar si sobre una se aplica una fuerza de pretensado mayor que sobre la otra?

Un saludo,
Manuel Aguilar.

Manuel Ballesta · Answer

Hola Manuel,

Si en la situación de servicio todas las fibras de la sección están comprimidas en todos los puntos de la barras. La rigidez de ambas barras (axil, flexión, corte, torsión), asumida misma sección y luz viene caracterizada por la sección homogeneizada que se parecerá mucho a la bruta.

Por lo tanto, ambas tienen la misma rigidez con independencia de que una esta más comprimida que la otra ya que ninguna a fisurado. Si tiene además la misma masa, tendrán la misma frecuencia natural y mismo comportamiento dinámico.

Saludos,
Manuel.

Manuel Ballesta · Answer

corrijo -> ha fisurado.

Juan Carlos Arroyo · Answer

Manuel Ballesta dixit!

Victor Alvado Benitez · Answer

Hola Manuel,

Vaya por delante que todo esto es muy teórico,! La inclusión de carga axil (como puede ser el pretensado) en la ecuación diferencial del movimiento modifica las frecuencias y modos propios, debido a la influencia del producto axil x curvatura.

Por comparar, la EDO de una viga "normal", sin el efecto de la carga axil es:

mientras que la EDO de una viga con el efecto de la carga axil es:

(con N+: tensión)

Como ves, aparece un término proporcional al axil, que cambia por completo la ecuación del movimiento y las frecuencias serán distintas según el valor de N. Para resolver estas EDOs, que ya es un poco "berenjenal", necesitas separar variables.

Espero que esto te ayude a aclarar el concepto!

Un saludo

Manuel Ballesta · Answer

Lo que apunta Víctor aquí es muy interesante. Una compresión en una barra imperfecta, podemos decir que por los efectos de segundo orden, flexibiliza la barra a cargas transversales, es decir, los momentos de segundo orden serán mayores que los de primer orden. Esta flexibilización o reducción de rigidez por la componente geométrica o de segundo orden será tanto más importante cuanto más cerca esté el axil de la barra del axil crítico de pandeo donde la barra se volvería un chicle a cargas transversales.

Ahora bien, volviendo a la realidad masiva del hormigón, ¿ Los pretensados introducidos en el hormigón pueden producir una reducción de la rigidez material por la componente geométrica del axil en elementos de hormigón pretensado ?. Desde luego, desde el punto científico el pretensado va a flexibilizar la rigidez material transversal pura reduciendo la misma por la componente geométrica. ¿ Podemos despreciar esta reducción ?. Creo que si, quizás me equivoco.

Saludos.

Victor Alvado Benitez · Answer

Manuel, desde un punto de vista más matemático, yo lo que entiendo que la ecuación nos quiere decir en su lenguaje es que no se trata de que al incluir el axil en la EDO del movimiento se reduzca la rigidez, sino que hay un efecto añadido que altera el equilibrio, como bien apuntas, un fenómeno de segundo orden debido al axil. De hecho, haciendo la ecuación independiente del tiempo (cargas estáticas), la EDO se convierte en la ecuación de pandeo. Y el problema que antes era de frecuencias de vibracion se convierte en un problema de carga crítica. Es innegable que este efecto tiene un cierto impacto a la hora de determinar las formas modales y por ende las frecuencias propias, y que a diferente axil, los resultados serán distintos. ¿Hasta donde influye el axil en las frecuencias? Pues no sé decirte, porque grosso modo, me parece un buen cacao (demasiado esfuerzo, poco beneficio) considerar todos estos efectos en unos cálculos en los que, entre otras mil cosas:Se desconoce el valor real del módulo de YoungLa inercia, como bien comenta Juan Carlos, depende del grado de fisuración (que depende del axil)El axil es variable (y si ya es difícil resolver el caso en axil constante, no te digo nada con axil variable...)La práctica normal, y la de referencias como Fryba, es la de directamente olvidarse del axil en estos casos y resolver la EDO de toda la vida, con inercias homogeneizadas: image.png 51.55 KBYo creo que no sale a cuenta volverse así de loco para afinar unas décimas de Hz unos cálculos que, por otra parte, también tienen sus limitaciones. Con unas buenas hipótesis, afinas más la frecuencia haciendo √(k/m) que resolviendo este tomate, bien la ecuación de manera numérica o bien en un MEF no lineal, que dan una falsa (y peligrosa) sensación de exactitud de la que hay que huir. Recomiendo encarecidamente el artículo de M. Alpañés al respecto (a mí me ayudó mucho): http://www.ciccp.es/webantigua/rop/Boletin/249/M_Alpa%C3%B1es.pdf. Pero es fantástico discutir estas cosas y contrastar opiniones, asique ¡espero debate! Un saludo, Victor

Manuel Ballesta · Answer

Hola Víctor, si no recuerdo mal la flecha por carga transversal bajo un cálculo de primer orden, se puede, de manera simplificada amplificar por el ratio 1/(1-N/Ncr) para obtener la flecha de segundo orden, N es el axil de la barra y Ncr es el axil crítico de pandeo elástico de la misma. Esto no es exacto, pero es una buena simplificación. Por lo tanto, un axil en la barra flexibiliza a la misma frente a cargas transversales. Gracias por lo que compartes, un abrazo. Manuel.

Manuel Aguilar García · Answer

Muchas gracias a todos, como siempre, por vuestras respuestas.

Carlos Rios Frutos · Answer

Hola a todos

Como esto me lo han preguntado en algún proyecto, creo que puedo aportar algo. El pretensado no induce efectos de 2 orden de ningún tipo, si es interior. Los efectos de 2 orden de un axil exterior o pretensado exterior tienen el efecto comentado, en Clough Penzien por ejemplo se habla muy claro del tema y en ciertos casos si podria ser significativo y se puede evaluar con programas de cálculo comerciales. Ahora bien, yo creo que la pregunta inicial es sobre cómo afinar una guitarra, pero a compresión. Y el asunto entonces no es el segundo orden, sino el tercero, es decir, la parte de funcionamiento de la viga como arco, cuerda si es una guitarra, bajo grandes deformaciones, que evidentemente es nula a efectos prácticos en vigas rectas salvo casos muy singulares, al contrario que en cuerdas de guitarra . Así que el cálculo estándar es correcto hasta el 4 o 5 decimal independienteme del nivel de pretensado. Si es un tirante de un puente, la frecuencia SI depende y absolutamente de la tensión. Es la cuerda de guitarra, vaya.

Manuel Ballesta · Answer

efectivamente, en un pretensado recto la pregunta es ... ¿ Es la curvatura de la deformada multiplicada por el pretensado superior a las cargas transversales? si no lo fuese ... se amplificaría la deformada por el axil (digamos cercano al crítico) hasta llegar a un punto donde se compensa y todo felicidad. ¿ ¿Pero que pasa si antes de llegar a este punto equilibrado nos cargamos la viga ? .

Manuel Ballesta · Answer

Jiri Strasky https://de.wikipedia.org/wiki/Trojsk%C3%A1_l%C3%A1vka#/media/Datei:Praha,_Trojsk%C3%A1_l%C3%A1vka,_den_po_z%C5%99%C3%ADcen%C3%AD_(03).jpg

Carlos Rios Frutos · Answer

Hola Manuel,

el tema es que el pretensado, si es interior, no induce efectos de segundo orden de ningún tipo. Los tendones se deforman con la viga, están siempre a la misma distancia y su momento es siempre el mismo. Otra forma de verlo es lo que comenta Fryba arriba, donde no dice que el efecto del axil de pretensado es pequeño y se desprecia, dice que no existe, en este caso recurriendo a que los esfuerzos en la sección son nulos si consideramos conjuntamente hormigón y acero activo, es decir sección completa, ya que es un estado tensional autoequilibrado, que es otra forma de ver que no hay esfuerzos de 2 orden debidos a pretensado interior. Ojo si es pretensado exterior, y solo si es exterior, si que hay efectos de segundo orden porque la linea que une anclajes o anclaje y desviador, que es la linea de acción de la fuerza del pretensado exterior, se aleja de la viga conforme está se deforma. Quizás te referías a este caso. El link que adjuntas es de una banda tesa, que precisamente es una "cuerda de guitarra".

Saludos

Manuel Ballesta · Answer

Toda la razón Carlos, en el concepto de la banda tesa que he compartido arriba, quería marcar que la rigidez del pasarela depende del pretensado pero porque este induce una forma o otra de más tendida de catenaria, pese a ser interior. Era una forma de intentar mostrar que el grado de pretensado influye en la rigidez de la misma, pero en este caso es por la forma, no por el pretensado en si mismo. Gracias!

José Manuel Soria Herrera · Answer

Debate muy interesante el de este post, poco puedo aportar ya a lo que se ha comentado.

Si que os dejo el link de un artículo que publicamos en la revista de Journal of Bridge Engenering de la ASCE, que trata sobre el estudio de la variación de las frecuencias de los modos de vibración de una pasarela banda tesa situada en Valladolid, proyectada por la oficina Carlos Fernández Casado. La conclusión es que por ser una banda tesa es muy sensible a la variación térmica y las frecuencias modales varían también mucho de forma inversamente proporcional a la temperatura.

Link: https://ascelibrary.org/doi/10.1061/%28ASCE%29BE.1943-5592.0000830

Si alguien no puede acceder y quisiera leerlo, que me escriba un correo (jm.soria@upm.es) y se lo envío sin problema.

Un saludo,
José Manuel

Análisis dinámico viga pretensada

Busca en todo ingenio.xyz cursos, lecciones, preguntas...

Busca en todo ingenio.xyz
cursos, lecciones, preguntas...